Phương pháp giải:

- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng định lí Pytago và định lí đường trung tuyến trong tam giác vuông tính độ dài các cạnh.

- Sử dụng định lí Cosin trong tam giác tính góc. Xác định chính xác góc giữa hai mặt phẳng là góc nhọn.

- Sử dụng công thức \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\,\,\forall \alpha \) để tính sin của góc giữa hai mặt phẳng.

Lời giải chi tiết:

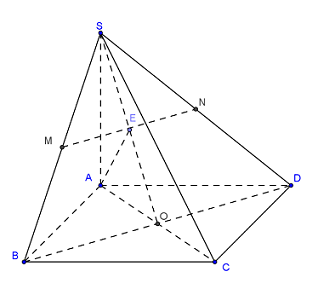
Gọi \(O\) là tâm của hình vuông \(ABCD\) \( \Rightarrow SO = \left( {SBD} \right) \cap \left( {SAC} \right).\)

Trong \(\left( {SAC} \right)\), gọi \(E = MN \cap SO\).

Vì \(MN\) là đường trung bình của tam giác \(SBD\)  nên \(MN\parallel BD\).

Ta có: \(\dfrac{{ME}}{{OB}} = \dfrac{{SE}}{{SO}} = \dfrac{{EN}}{{OD}}\) (Định lí Ta-lét), mà \(OB = OD\) nên \(ME = EN\) hay \(E\) là trung điểm của \(MN\).

Xét \(\Delta SAB\) và \(\Delta SAD\) có:

\(\angle SAB = \angle SAD = {90^0}\),

\(SA\) chung;

\(AB = AD\,\,\,\left( {gt} \right)\).

\( \Rightarrow \Delta SAB = \Delta SAD\) (hai cạnh góc vuông).

\( \Rightarrow AM = AN\) (2 trung tuyến tương ứng) và \(SB = SD\) (hai cạnh tương ứng).

\( \Rightarrow \Delta AMN\) cân tại \(A\) \( \Rightarrow AE \bot MN\) (trung tuyến đồng thời là đường cao).

Lại có \(\Delta SBD\) cân tại \(S\) \( \Rightarrow SO \bot MN\) (trung tuyến đồng thời là đường cao).

Ta có: \(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {SBD} \right) = MN\\\left( {AMN} \right) \supset AE \bot MN\\\left( {SBD} \right) \supset SO \bot MN\end{array} \right.\)\(MN//BD\, \bot \left( {SAC} \right) \Rightarrow \)\( \Rightarrow \angle \left( {\left( {AMN} \right);\left( {SBD} \right)} \right) = \angle \left( {AE;SO} \right)\)

Ta có: \(\dfrac{{SE}}{{SO}} = \dfrac{{SM}}{{SB}} = \dfrac{1}{2} \Rightarrow E\) là trung điểm của \(SO\).

Xét tam giác \(SAO\), \(E\) là trung điểm của \(SO\) có:

\(\begin{array}{l}SA = a,\,AO = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\\ \Rightarrow SO = \sqrt {S{A^2} + A{O^2}}  = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 6 }}{2}\\ \Rightarrow AE = EO = \dfrac{1}{2}SO = \dfrac{{a\sqrt 6 }}{4}.\end{array}\)

Tam giác \(AEO\) có: \({\rm{cos}}\angle AEO = \dfrac{{A{E^2} + E{O^2} - A{O^2}}}{{2.AE.EO}} = \dfrac{{\dfrac{{3{a^2}}}{8} + \dfrac{{3{a^2}}}{8} - \dfrac{{{a^2}}}{2}}}{{2.\dfrac{{3{a^2}}}{8}}} = \dfrac{1}{3} > 0.\)

\( \Rightarrow \angle AEO\) là góc nhọn \( \Rightarrow \angle \left( {\left( {AMN} \right);\left( {SBD} \right)} \right) = \angle AEO\).

Ta có:  \(\sin \angle AEO = \sqrt {1 - {{\cos }^2}\angle AEO}  = \dfrac{{2\sqrt 2 }}{3}.\)

Vậy \(\sin \angle \left( {\left( {AMN} \right);\left( {SBD} \right)} \right) = \dfrac{{2\sqrt 2 }}{3}\).

Chọn B.

Số đo góc giữa hai mặt phẳng luôn nhỏ hơn hoặc bằng \({90^0}\).