Phương pháp giải:

Diện tích hình chiếu của một đa giác: Cho đa giác H thuộc \(\left( \alpha  \right)\). Gọi đa giác H’ là hình chiếu của đa giác H lên \(\left( \beta  \right)\); \(\varphi \)= là góc giữa \(\left( \alpha  \right)\) và \(\left( \beta  \right)\).  Khi đó : \({S_{\left( {H'} \right)}} = {\rm{cos}}\alpha {\rm{. }}{{\rm{S}}_{\left( H \right)}}\)

Lời giải chi tiết:

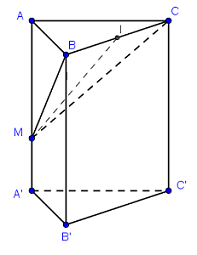
Gọi \(\varphi \) là góc giữa mp(ABC) và mp(MBC).

Tam giác ABC là hình chiếu của tam giác MBC lên (ABC) \( \Rightarrow {\rm{cos}}\varphi  = \dfrac{{{S_{ABC}}}}{{{S_{MBC}}}}\)

Ta có: \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Tam giác MBC cân tại M có: \(MB = MC = \sqrt {A{B^2} + A{M^2}}  = \sqrt {{a^2} + {{\left( {\dfrac{{3{\rm{a}}}}{4}} \right)}^2}}  = \dfrac{{5{\rm{a}}}}{4}\)

Gọi I là trung điểm của BC \( \Rightarrow MI = \sqrt {M{B^2} - {{\left( {\dfrac{{BC}}{2}} \right)}^2}}  = \sqrt {{{\left( {\dfrac{{5{\rm{a}}}}{4}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}}  = \dfrac{{a\sqrt {21} }}{4}\)

\( \Rightarrow {S_{MBC}} = \dfrac{1}{2}.MI.BC = \dfrac{1}{2}.\dfrac{{a\sqrt {21} }}{4}.a = \dfrac{{{a^2}\sqrt {21} }}{8}\)\(y = 4\)

\( \Rightarrow {\rm{cos}}\varphi  = \dfrac{{{S_{ABC}}}}{{{S_{MBC}}}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{4}}}{{\dfrac{{{a^2}\sqrt {21} }}{8}}} = \dfrac{2}{{\sqrt 7 }}\)\( \Rightarrow {\tan ^2}\varphi  = \dfrac{1}{{{\rm{co}}{{\rm{s}}^2}\varphi }} - 1 = \dfrac{3}{4} \Rightarrow \tan \varphi  = \dfrac{{\sqrt 3 }}{2}.\)

Chọn A.