Câu hỏi:
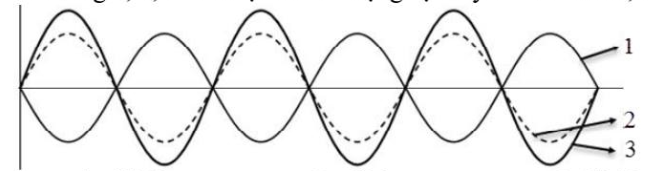
Hình vẽ dưới đây biểu diễn hình dạng của một sợi dây đang có sóng dừng với tần số f = 20 Hz. Biết các đường 3, 2, 1 lần lượt là hình dạng sợi dây ở thời điểm t, t + Δt, t + 3Δt. Giá trị của Δt nhỏ nhất là
- A \(\dfrac{{\rm{1}}}{{{\rm{160}}}}\,\,{\rm{s}}\)
- B \(\dfrac{{\rm{1}}}{{{\rm{80}}}}\,\,{\rm{s}}\)
- C \(\dfrac{{\rm{1}}}{{{\rm{240}}}}\,\,{\rm{s}}\)
- D \(\dfrac{{\rm{1}}}{{{\rm{120}}}}\,\,{\rm{s}}\)
Phương pháp giải:
Sử dụng lý thuyết về sóng dừng.
Lời giải chi tiết:
Khoảng thời gian từ vị trí ứng với đường 2 qua vị trí ứng với đường 3 là:
\(\left( {{\rm{t + 3\Delta t}}} \right) - \left( {{\rm{t + \Delta t}}} \right){\rm{ = 2\Delta t}}\)
Xét \({\rm{\Delta t}}\) nhỏ nhất thì từ vị trí đường số 2 về vị trí cân bằng dây duỗi thẳng là \({\rm{\Delta t}}\)
Thời gian từ vị trí ứng với đường số 1 đến vị trí cân bằng dây duỗi thẳng là:
\({\rm{2\Delta t = }}\dfrac{{\rm{T}}}{{\rm{4}}} \Rightarrow {\rm{\Delta t = }}\dfrac{{\rm{T}}}{{\rm{8}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{8f}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{8}}{\rm{.20}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{160}}}}\,\,\left( {\rm{s}} \right)\)
Chọn A.


















