Câu hỏi:
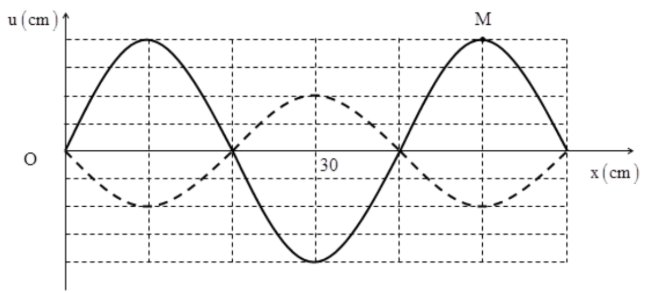
Một sợi dây đàn hồi căng ngang hai đầu cố định AB đang có sóng dừng ổn định với tần số f. Hình vẽ mô tả dạng của sợi dây tại thời điểm t1 (nét liền) và thời điểm \({t_2} = {t_1} + \dfrac{2}{3}\,\,s\) (nét đứt). Biết rằng thời điểm t1, điểm M có tốc độ bằng 0 và hướng về vị trí cân bằng của nó. Tốc độ truyền sóng trên dây có thể là
- A 30 cm/s
- B 35 cm/s
- C 50 cm/s
- D 40 cm/s
Phương pháp giải:
Áp dụng kĩ năng đọc đồ thị
Sử dụng vòng tròn lượng giác và công thức: \(\omega = \dfrac{{\Delta \varphi }}{{\Delta t}}\)
Tốc độ truyền sóng trên dây: \(v = \lambda .f = \lambda .\dfrac{\omega }{{2\pi }}\)
Lời giải chi tiết:
Từ đồ thị ta thấy: \(\dfrac{3}{4}\lambda = 30 \Rightarrow \lambda = 40\,\,\left( {cm} \right)\)
Xét dao động của điểm M, tại thời điểm t1 có li độ: \({u_{1M}} = A\)
Ở thời điểm t2, li độ của điểm M là: \({u_{2M}} = - \dfrac{A}{2}\) và đang hướng về vị trí cân bằng
Vậy trong thời gian \(\Delta t = {t_2} - {t_1} = \dfrac{2}{3}\,\,\left( s \right)\), điểm M đi từ biên dương tới biên âm rồi tới li độ \({u_{2M}} = - \dfrac{A}{2}\)
Ta có vòng tròn lượng giác:
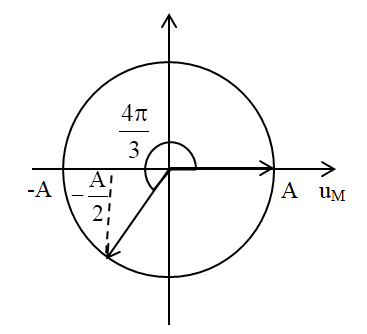
Từ vòng tròn lượng giác, ta thấy trong khoảng thời gian \(\Delta t\), vecto quay được góc: \(\Delta \varphi = \dfrac{{4\pi }}{3}\,\,\left( {rad} \right)\)
Tần số góc của sóng là: \(\omega = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{{4\pi }}{3}}}{{\dfrac{2}{3}}} = 2\pi \,\,\left( {rad/s} \right)\)
Tốc độ truyền sóng trên dây là: \(v = \lambda .\dfrac{\omega }{{2\pi }} = 40.\dfrac{{2\pi }}{{2\pi }} = 40\,\,\left( {cm/s} \right)\)
Chọn D.


















