Phương pháp giải:

Khoảng cách giữa hai điểm nút và bụng gần nhau nhất: \(\dfrac{\lambda }{4}\)

Biên độ của điểm cách nút sóng khoảng x: \({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right|\)

Sử dụng vòng tròn lượng giác và công thức: \(\omega  = \dfrac{{\Delta \varphi }}{{\Delta t}}\)

Tốc độ truyền sóng: \(v = \lambda f = \lambda .\dfrac{\omega }{{2\pi }}\)

Lời giải chi tiết:

Khoảng cách AB là: \(\dfrac{\lambda }{4} = AB = 10 \Rightarrow \lambda  = 40\,\,\left( {cm} \right)\)

Khoảng cách AC là: \(x = AC = \dfrac{{AB}}{2} = \dfrac{{10}}{2} = 5\,\,\left( {cm} \right)\)

Biên độ dao động của điểm C là:

\({A_C} = {A_B}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| = {A_B}.\left| {\sin \dfrac{{2\pi .5}}{{40}}} \right| = {A_B}.\dfrac{{\sqrt 2 }}{2}\)

Ta có vòng tròn lượng giác:

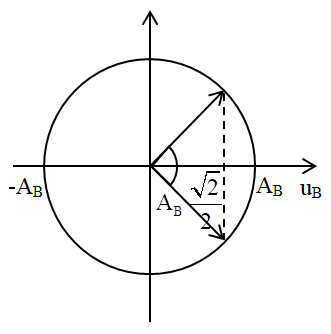
Từ vòng tròn lượng giác, ta thấy khoảng thời gian ngắn nhất giữa hai lần li độ của điểm B bằng biên độ của điểm C, vecto quay được góc: \(\Delta \varphi  = \dfrac{\pi }{4}\,\,\left( {rad} \right)\)

Tần số góc của sóng là: \(\omega  = \dfrac{{\Delta \varphi }}{{\Delta t}} = \dfrac{{\dfrac{\pi }{4}}}{{0,2}} = 1,25\pi \,\,\left( {rad/s} \right)\)

Tốc độ truyền sóng là: \(v = \lambda f = \lambda .\dfrac{\omega }{{2\pi }} = 40.\dfrac{{1,25\pi }}{{2\pi }} = 25\,\,\left( {cm/s} \right) = 0,25\,\,\left( {m/s} \right)\)

Chọn A.