Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại A và B, \(AB = BC = a,\,AD = 2a\). Biết \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\) và \(SA = a\). Gọi \(M,N\) lần lượt là trung điểm \(SB,CD\). Tính sin của góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {SAC} \right)\).
- A \(\dfrac{{2\sqrt 5 }}{5}\).
- B \(\dfrac{{3\sqrt 5 }}{{10}}\).
- C \(\dfrac{{\sqrt 5 }}{5}\).
- D \(\dfrac{{\sqrt {55} }}{{10}}\).
Phương pháp giải:
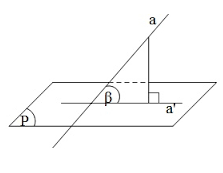
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Lời giải chi tiết:
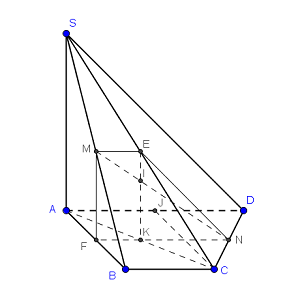
Gọi E, F lần lượt là trung điểm của SC, AB. Dễ dàng chứng minh được MENF là hình thang vuông (ME//NF, \(\angle M = \angle F = {90^0}\))
Gọi K là giao điểm của NF và AC, I là giao điểm của EK và MN. Khi đó, I chính là giao điểm của MN và (SAC)
Do \(\left\{ \begin{array}{l}NC \bot AC\\NC \bot SA\end{array} \right. \Rightarrow NC \bot \left( {SAC} \right)\) và C là hình chiếu vuông góc của N lên (SAC) \( \Rightarrow \angle \left( {MN;\left( {SAC} \right)} \right) = \angle NIC\)
Tam giác NIC vuông tại C \( \Rightarrow \sin NIC = \dfrac{{NC}}{{IN}}\)
Ta có: \(NC = \dfrac{1}{2}CD = \dfrac{1}{2}.\sqrt {{a^2} + {a^2}} = \dfrac{{a\sqrt 2 }}{2}\),
\(MN = \sqrt {M{F^2} + N{F^2}} = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{3{\rm{a}}}}{2}} \right)}^2}} = \dfrac{{a\sqrt {10} }}{2}\),
\(\dfrac{{IN}}{{IM}} = \dfrac{{KN}}{{ME}} = 2 \Rightarrow IN = \dfrac{2}{3}MN = \dfrac{2}{3}.\dfrac{{a\sqrt {10} }}{2} = \dfrac{{a\sqrt {10} }}{3}\)\( \Rightarrow \sin NIC = \dfrac{{NC}}{{IN}} = \dfrac{{3\sqrt 5 }}{{10}}\)
Vậy, sin của góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {SAC} \right)\) là: \(\dfrac{{3\sqrt 5 }}{{10}}\).
Chọn B.


















