Phương pháp giải:

- Chuyển tính khoảng cách từ $M$ đến mặt phẳng $\left( {SAC} \right)$ sang tính khoảng cách từ $H$ đến $\left( {SAC} \right)$.

- Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

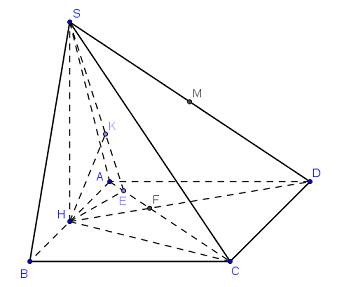
Gọi $H$ là trung điểm của $AB$.

Vì $\Delta SAB$ cân tại $S$ nên $SH \bot AB$.

Ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\end{array} \right.$ $\Rightarrow SH \bot \left( {ABCD} \right)$.

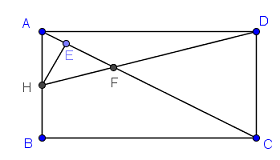
Trong $\left( {ABCD} \right)$ gọi $F = AC \cap HD$, dựng $HE \bot AC$ ta có: $\left\{ \begin{array}{l}AC \bot HE\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right)$.

Trong $\left( {SHE} \right)$ kẻ $HK \bot SE$ ta có: $\left\{ \begin{array}{l}HK \bot SE\\HK \bot AC\end{array} \right. \Rightarrow HK \bot \left( {SAC} \right)$$\Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HK$.

Ta có: $M$ là trung điểm của $SC$ $\Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \dfrac{1}{2}d\left( {D;\left( {SAC} \right)} \right)$

Lại có:  $\dfrac{{DF}}{{HF}} = \dfrac{{DC}}{{HA}} = 2$ $\Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)$

$\Rightarrow d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right) = HK$

Ta có: $\Delta AHE$ đồng dạng $\Delta ACB$ $\left( {g.g} \right)$.

$\Rightarrow \dfrac{{HE}}{{BC}} = \dfrac{{AH}}{{AC}} \Leftrightarrow \dfrac{{HE}}{{2a}} = \dfrac{{\dfrac{a}{2}}}{{\sqrt {{a^2} + 4{a^2}} }} \Leftrightarrow HE = \dfrac{{a\sqrt 5 }}{5}$

Ta có : $SH \bot \left( {ABCD} \right)$ nên $HC$ là hình chiếu của $SC$ lên $\left( {ABCD} \right)$.

$\Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}$.

$\Delta BHC$ vuông  tại $B$ $\Rightarrow HC = \sqrt {B{C^2} + B{H^2}}  = \sqrt {4{{\rm{a}}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}}  = \dfrac{{a\sqrt {17} }}{2}$

$\Delta SHC$ vuông tại $H$ $\Rightarrow SH = HC.\tan {45^0} = \dfrac{{a\sqrt {17} }}{2}$

Tam giác SHE vuông tại H, HK là đường cao

$\Rightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}} = \dfrac{1}{{\dfrac{{17{{\rm{a}}^2}}}{4}}} + \dfrac{1}{{\dfrac{{{a^2}}}{5}}} = \dfrac{{89}}{{17{{\rm{a}}^2}}} \Rightarrow HK = \dfrac{{a\sqrt {1513} }}{{89}}$

$\Rightarrow d\left( {M;\left( {SAC} \right)} \right) = d = \dfrac{{a\sqrt {1513} }}{{89}}.$

Chọn:  A.