Phương pháp giải:

- Xác định góc giữa cạnh bên \(SD\) và mặt đáy \(\left( {ABCD} \right)\) là góc giữa \(SD\) và hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\)

- Đổi khoảng cách từ \(d\left( {B;\left( {SCD} \right)} \right)\) sang \(d\left( {H;\left( {SCD} \right)} \right)\) với \(H\) là chân đường cao của khối chóp, sử dụng công thức: \(\dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{BM}}{{HM}}\) với \(M = BH \cap \left( {SCD} \right)\).

- Xác định khoảng cách từ \(H\) đến \(\left( {SCD} \right)\). Áp dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

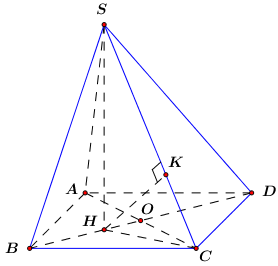
Gọi \(H\) là trọng tâm tam giác đều \(ABC\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).

\( \Rightarrow HD\) là hình chiếu của \(SD\) lên \(\left( {ABCD} \right)\).

\( \Rightarrow \angle \left( {SD;\left( {ABCD} \right)} \right) = \angle \left( {SD;HD} \right) = \angle SDH = {30^0}\).

Ta có: \(\dfrac{{BH}}{{BO}} = \dfrac{2}{3} \Rightarrow \dfrac{{BH}}{{BD}} = \dfrac{1}{3} \Rightarrow \dfrac{{HD}}{{BD}} = \dfrac{2}{3}\).

Mà \(BH \cap \left( {SCD} \right) = D\)\( \Rightarrow \dfrac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \dfrac{{BD}}{{HD}} = \dfrac{3}{2}\)\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}d\left( {H;\left( {SCD} \right)} \right)\).

Ta có \(H\) là trọng tâm tam giác đều \(ABC\)nên \(HC \bot AB\). Mà \(AB\parallel CD\) nên \(HC \bot CD\).

Trong \(\left( {SHC} \right)\) kẻ \(HK \bot SC\).

Ta có \(\left\{ \begin{array}{l}CD \bot CH\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHC} \right)\) \( \Rightarrow CD \bot HK\).

\(\left\{ \begin{array}{l}HK \bot SC\\HK \bot CD\end{array} \right. \Rightarrow HK \bot \left( {SCD} \right)\) \( \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\).

Vì tam giác \(ABC\) đều cạnh \(a\) nên \(HC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).

Ta có: \(\dfrac{{HD}}{{BD}} = \dfrac{2}{3}\), mà \(BD = 2BO = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \)\( \Rightarrow HD = \dfrac{2}{3}BD = \dfrac{{2a\sqrt 3 }}{3}\)

Xét tam giác vuông \(SHD\) ta có: \(SH = HD.\tan {30^0} = \dfrac{{2a\sqrt 3 }}{3}.\dfrac{{\sqrt 3 }}{3} = \dfrac{{2a}}{3}.\)

Áp dụng hệ thức lượng trong tam giác vuông \(SHC\) ta có: \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{C^2}}} = \dfrac{1}{{\dfrac{{4{a^2}}}{9}}} + \dfrac{1}{{\dfrac{{{a^2}}}{3}}} = \dfrac{{21}}{{4a^2}}.\)

\( \Rightarrow HK = \dfrac{{2\sqrt {21} }}{{21}}a\)

Vậy \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{3}{2}HK = \dfrac{{3\sqrt {21} }}{{21}}a\).

Chọn C.