Phương pháp giải:

- Các mặt bên của hình chóp cùng tạo với đáy 1 số đo góc \( \Rightarrow \) Hình chiếu vuông góc của đỉnh S đến mặt đáy là tâm đường tròn nội tiếp đa giác đáy.

Lời giải chi tiết:

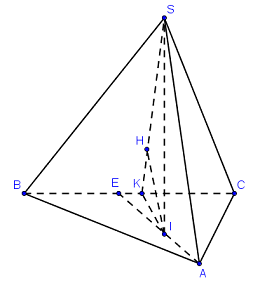
Gọi \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\).

Do các mặt phẳng \(\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)\) cùng tạo với đáy \(\left( {ABC} \right)\) một góc \({60^0}\)\( \Rightarrow SI \bot \left( {ABC} \right).\)

Trong \(\Delta ABC\) gọi \(AE\) là phân giác \(\left( {E \in BC} \right)\) ta có:

\(\begin{array}{l} \Rightarrow \dfrac{{AC}}{{AB}} = \dfrac{{EC}}{{EB}} \Rightarrow \dfrac{{AC}}{{AC + AB}} = \dfrac{{EC}}{{BC}}\\ \Rightarrow \dfrac{{{\rm{3}}a}}{{3a + 4a}} = \dfrac{{EC}}{{5a}} \Rightarrow EC = \dfrac{{15a}}{7}\end{array}\)

Xét \(\Delta AEC\) có \(CI\) là phân giác

\(\begin{array}{l} \Rightarrow \dfrac{{AC}}{{EC}} = \dfrac{{IA}}{{IE}} \Rightarrow \dfrac{{3a}}{{\dfrac{{15a}}{7}}} = \dfrac{{IA}}{{IE}}\\ \Rightarrow \dfrac{{AE}}{{IE}} = \dfrac{{3a + \dfrac{{15a}}{7}}}{{\dfrac{{15a}}{7}}} = \dfrac{{\dfrac{{{\rm{36}}a}}{7}}}{{\dfrac{{15a}}{7}}} \Rightarrow \dfrac{{AE}}{{IE}} = \dfrac{{12}}{5}\end{array}\)

\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{12}}{5}d\left( {I;\left( {SBC} \right)} \right)\)

Kẻ \(IK \bot BC,\,\,\left( {K \in BC} \right),\,\,IH \bot \left( {SBC} \right),\left( {H \in SK} \right) \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow d\left( {I;\left( {SBC} \right)} \right) = IH\)

Đồng thời, \(IK = r\) : bán kính đường tròn nội tiếp tam giác ABC và \(\angle IKS = \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = {60^0}\)

Tam giác ABC có : \(S = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3a.4a = 6{a^2}\) (do tam giác ABC vuông tại A)

\(S = \dfrac{1}{2}\left( {AB + AC + BC} \right).r\)\( = \dfrac{1}{2}.\left( {3a + 4a + 5a} \right).r = 6a.r\)\( \Rightarrow 6ar = 6{a^2} \Rightarrow r = a\) 

Tam giác IHK có : \(IH = IK.\sin {60^0} = a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = \dfrac{{12}}{5}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{\rm{6a}}\sqrt 3 }}{5}\).

Chọn D.