Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B;\)\(AB = BC = 1\), \(AD = 2\). Các mặt chéo \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) cùng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Biết góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^0}\) (tham khảo hình vẽ bên). Khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\) là
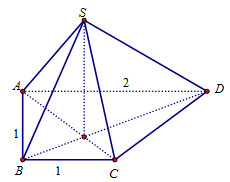
- A \(\dfrac{{2\sqrt 3 }}{3}\)
- B \(\sqrt 3 \).
- C \(2\sqrt 3 \).
- D \(\dfrac{{\sqrt 3 }}{3}\).
Phương pháp giải:
Lời giải chi tiết:
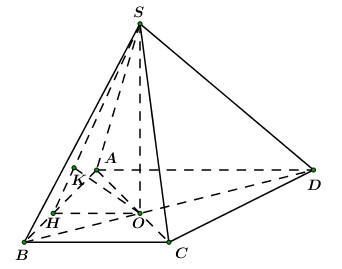
Gọi O là giao điểm của AC và BD.
\( \Rightarrow SO \bot \left( {ABCD} \right).\)
Qua O, kẻ đường thẳng vuông góc với AB, cắt AB tại H.
Ta có: \(\left\{ \begin{array}{l}OH \bot AB\\SO \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SAB} \right) \Rightarrow SH \bot AB.\)
\( \Rightarrow \angle \left( {\left( {SAB} \right),\,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SH,\,\,HO} \right) = \angle SHO = {60^0}.\)
Ta có: \(BC//AD,\) áp dụng định lý Ta-let ta có:
\(\begin{array}{l}\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}} = \frac{{AD}}{{BC}} = 2\\ \Rightarrow \left\{ \begin{array}{l}OA = 2OC\\OD = 2OB\end{array} \right.\end{array}\)
Lại có:\(OA + OC = \sqrt 2 \) \( \Rightarrow \frac{3}{2}OA = \sqrt 2 \Rightarrow OA = \frac{{2\sqrt 2 }}{3}.\)
\( \Rightarrow AH = OH = \frac{{OA}}{{\sqrt 2 }} = \frac{2}{3}.\)
\( \Rightarrow SO = OH.\tan {60^0} = \frac{{2\sqrt 3 }}{3}.\)
Ta có: \(\frac{{DB}}{{OB}} = \frac{{d\left( {D;\,\,\left( {SAB} \right)} \right)}}{{d\left( {O;\,\,\left( {SAB} \right)} \right)}} = 3\) \( \Rightarrow d\left( {D;\,\,\left( {SAB} \right)} \right) = 3d\left( {O;\,\,\left( {SAB} \right)} \right).\)
Từ O dựng đường thẳng vuông góc với SH tại K.
\( \Rightarrow OK \bot \left( {SAB} \right) \Rightarrow d\left( {O;\,\,\left( {SAB} \right)} \right) = OK.\)
Áp dụng hệ thức lượng trong tam giác SOH vuông tại O có đường cao OK ta có:
\(\begin{array}{l}OK = \frac{{OH.SO}}{{\sqrt {O{H^2} + S{O^2}} }} = \frac{{\frac{2}{3}.\frac{{2\sqrt 3 }}{3}}}{{\sqrt {\frac{4}{9} + \frac{4}{3}} }} = \frac{{\frac{{4\sqrt 3 }}{9}}}{{\frac{4}{3}}} = \frac{{\sqrt 3 }}{3}.\\ \Rightarrow d\left( {D;\,\,\left( {SAB} \right)} \right) = \sqrt 3 .\end{array}\)
Chọn B.


















