Phương pháp giải:

Suy luận từng đáp án, sử dụng phương pháp chứng minh đường thẳng vuông góc với mặt phẳng: $\left\{ \begin{array}{l}a \bot b\\a \bot c\\b \cap c \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)$ và phương pháp chứng minh đường vuông góc với mặt: $\left\{ \begin{array}{l}d \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a$.

Lời giải chi tiết:

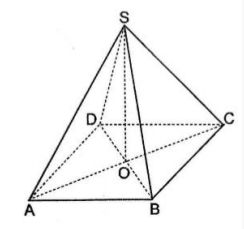
Ta có: $SO \bot AC$ (do tam $SAC$ cân tại $S$)

$SO \bot BD$(do tam $SBD$ cân tại $S$)

$\Rightarrow SO \bot \left( {ABCD} \right)$ $\Rightarrow$ Đáp án B đúng.

Ta có: $\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot SD \Rightarrow$Đáp án A đúng

Tương tự: $\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BD \bot SA$ $\Rightarrow$ Đáp án D đúng.

Chọn: C.