Câu hỏi:
Tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ABD\) là các tam giác đều. Góc giữa \(AB\) và \(CD\) là:
- A \({60^0}\).
- B \({30^0}\).
- C \({90^0}\).
- D \({120^0}\).
Phương pháp giải:
\(\left\{ \begin{array}{l}a \bot b,\,a \bot c\\b,c \subset \left( \alpha \right)\\b \cap c = \left\{ I \right\}\end{array} \right. \Rightarrow a \bot \left( \alpha \right)\) ; \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\\forall b,\,\,b \subset \left( \alpha \right)\end{array} \right. \Rightarrow a \bot b\)
Lời giải chi tiết:
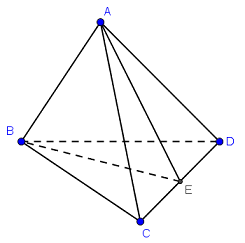
Gọi \(E\) là trung điểm của \(CD\).
Vì \(ABC\) và \(ABD\) là các tam giác đều nên \(AB = AC = AD = BC = BD.\)
\( \Rightarrow \Delta ACD,\,\,\Delta BCD\) cân lần lượt tại các đỉnh \(A,\,\,B\).
\( \Rightarrow \left\{ \begin{array}{l}AE \bot CD\\BE \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABE} \right) \Rightarrow CD \bot AB\)
\( \Rightarrow \left( {AB;CD} \right) = {90^0}.\)
Chọn C.


















