Phương pháp giải:

Lời giải chi tiết:

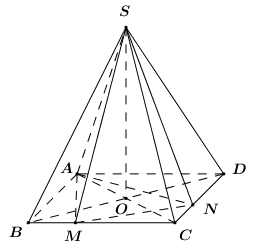
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

Do \(ABCD\) là hình vuông cạnh bằng \(1\) nên \(AC = BD = \sqrt 2 \)\( \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{\sqrt 2 }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông \(SOA\) ta có: \(SO = \sqrt {S{A^2} - O{A^2}}  = \dfrac{{\sqrt 2 }}{2}\).

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot \left( {AMN} \right)\).

\( \Rightarrow {V_{S.AMN}} = \dfrac{1}{3}SO.{S_{AMN}} = \dfrac{{\sqrt 2 }}{6}.{S_{AMN}}\).

Do đó \({V_{S.AMN\,\,\min }} \Leftrightarrow {S_{AMN}}\) min.

Đặt \(CM = x,\,\,CN = y\,\,\left( {0 \le x;y \le 1} \right)\), khi đó ta có \({x^2} + {y^2} = 1\) (Định lí Pytago trong tam giác vuông \(CMN\)).

Ta có

\(\begin{array}{l}{S_{ABM}} = \dfrac{1}{2}AB.AM = \dfrac{1}{2}\left( {1 - x} \right)\\{S_{ADN}} = \dfrac{1}{2}AD.DN = \dfrac{1}{2}\left( {1 - y} \right)\\{S_{CMN}} = \dfrac{1}{2}xy\\ \Rightarrow {S_{AMN}} = {S_{ABCD}} - \left( {{S_{ABM}} + {S_{ADN}} + {S_{CMN}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 - \dfrac{1}{2}\left( {1 - x + 1 - y + xy} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 - \dfrac{1}{2}\left( {2 - x - y + xy} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {x + y - xy} \right)\end{array}\)

Ta có \({x^2} + {y^2} = 1 \Leftrightarrow y = \sqrt {1 - {x^2}} \). Khi đó ta có \(S = \dfrac{1}{2}\left( {x + \sqrt {1 - {x^2}}  - x\sqrt {1 - {x^2}} } \right)\).

Xét hàm số \(f\left( x \right) = x + \sqrt {1 - {x^2}}  - x\sqrt {1 - {x^2}} \) với \(x \in \left( {0;1} \right)\) ta có:

\(\begin{array}{l}y' = 1 - \dfrac{x}{{\sqrt {1 - {x^2}} }} - \sqrt {1 - {x^2}}  - x.\dfrac{{ - x}}{{\sqrt {1 - {x^2}} }}\\y' = \dfrac{{\sqrt {1 - {x^2}}  - x - \left( {1 - {x^2}} \right) + {x^2}}}{{\sqrt {1 - {x^2}} }}\\y' = \dfrac{{\sqrt {1 - {x^2}}  + 2{x^2} - x - 1}}{{\sqrt {1 - {x^2}} }}\end{array}\)

\(\begin{array}{l}y' = 0 \Leftrightarrow \sqrt {1 - {x^2}}  + 2{x^2} - x - 1 = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \sqrt {\left( {1 - x} \right)\left( {1 + x} \right)}  + \left( {x - 1} \right)\left( {2x + 1} \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \sqrt {1 - x} \left[ {\sqrt {1 + x}  - \sqrt {1 - x} \left( {2x + 1} \right)} \right] = 0\\\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\\sqrt {1 + x}  - \sqrt {1 - x} \left( {2x + 1} \right) = 0\end{array} \right.\\\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\1 + x = \left( {1 - x} \right){\left( {2x + 1} \right)^2}\end{array} \right.\\\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\4{x^3} - 2x = 0\end{array} \right.\\\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\\x = \dfrac{1}{{\sqrt 2 }}\end{array} \right.\end{array}\)

BBT:

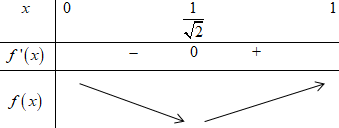
Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = f\left( {\dfrac{{\sqrt 2 }}{2}} \right) = \dfrac{{2\sqrt 2  - 1}}{4}\).

\( \Rightarrow \min {S_{AMN}} = \dfrac{{2\sqrt 2  - 1}}{4}\).

Vậy \(\min {V_{S.AMN}} = \dfrac{{\sqrt 2 }}{6}.\dfrac{{2\sqrt 2  - 1}}{4} = \dfrac{{4 - \sqrt 2 }}{{24}}\) 

Chọn D.