Câu hỏi:
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), \(AB = 2a\), \(\angle BAC = {120^0}\), \(\angle SBA = \angle SCA = {90^0}\). Biết góc giữa \(SB\) và đáy bằng \({60^0}\). Tính thể tích \(V\) của khối chóp \(S.ABC\).
- A \(6\sqrt 3 {a^3}\)
- B \(6{a^3}\)
- C \(2{a^3}\)
- D \(2\sqrt 3 {a^3}\)
Phương pháp giải:
- Gọi \(M\) là trung điểm của \(SA\), chứng minh \(MA = MB = MC\) , từ đó xác định hình chiếu của \(M\) trên \(\left( {ABC} \right)\).
- Xác định hình chiếu của \(S\) lên \(\left( {ABC} \right)\).
- Xác định góc giữa \(SB\) và \(\left( {ABC} \right)\) bằng góc giữa \(SB\) và hình chiếu của \(SB\) lên \(\left( {ABC} \right)\).
- Sử dụng định lí Cosin trong tam giác, tỉ số lượng giác của góc nhọn tính \(SH\).
- Sử dụng công thức tính diện tích tam giác \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC.\sin \angle BAC\).
- Áp dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
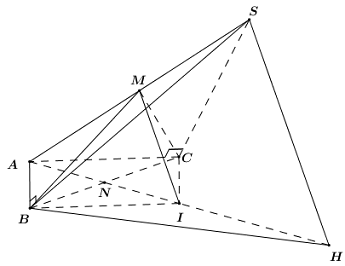
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA,\,\,BC\).
Ta có: \(\Delta SAB,\,\,\Delta SAC\) lần lượt vuông tại \(B,\,\,C\) nên \(BM = CM = \dfrac{1}{2}SA = MS = MA\).
\( \Rightarrow \) Chóp \(M.ABC\) có \(MA = MB = MC\) nên hình chiếu của \(M\) lên \(\left( {ABC} \right)\) trùng với tâm đường tròn ngoại tiếp tam giác \(ABC\).
Dựng hình bình hành \(ABIC\) ta có: \(IB = AC = 2a,\,\,IC = AB = 2a\).
Tam giác \(ABC\) cân tại \(A\) nên \(AN \bot BC\) (Trung tuyến đồng thời là đường cao) và \(\angle BAN = {60^0}\) (Trung tuyến đồng thời là đường phân giác).
Xét tam giác vuông \(ABN\) có \(AN = AB.\cos {60^0} = a\).
\( \Rightarrow AI = 2AN = 2a\).
Do đó \(IA = IB = IC = 2a\) nên \(I\) là tâm đường tròn ngoại tiếp \(\Delta ABC\).
\( \Rightarrow MI \bot \left( {ABC} \right)\).
Trong \(\left( {AMI} \right)\) lẻ \(SH\parallel MI\,\,\left( {H \in AI} \right)\) ta có \(SH \bot \left( {ABC} \right)\).
\( \Rightarrow HB\) là hình chiếu của \(SB\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;HB} \right) = \angle SBH = {60^0}\).
Xét tam giác \(SAH\) có: \(M\) là trung điểm của \(SA\), \(SH\parallel MI\) nên \(I\) là trung điểm của \(AH\) (Định lí đường trung bình).
\( \Rightarrow AH = 2AI = 4a\).
Áp dụng định lí Cosin trong tam giác \(ABH\) ta có:
\(\begin{array}{l}B{H^2} = A{B^2} + A{H^2} - 2AB.AH.\cos {60^0}\\B{H^2} = {\left( {2a} \right)^2} + {\left( {4a} \right)^2} - 2.2a.4a.\dfrac{1}{2}\\B{H^2} = 12{a^2}\\ \Rightarrow BH = 2a\sqrt 3 \end{array}\)
Xét tam giác vuông \(SBH\) có: \(SH = BH.\tan {60^0} = 6a\).
\({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC.\sin \angle BAC\)\( = \dfrac{1}{2}.2a.2a.\sin {120^0} = {a^2}\sqrt 3 \).Vậy \({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}}\)\( = \dfrac{1}{3}.6a.{a^2}\sqrt 3 = 2{a^3}\sqrt 3 \).
Chọn D.


















