Phương pháp giải:

- Xác định góc giữa mặt bên và đáy.

- Sử dụng công thức thể tích tính chiều cao của khối chóp.

- Áp dụng các tỉ số lượng giác của góc nhọn trong tam giác vuông.

Lời giải chi tiết:

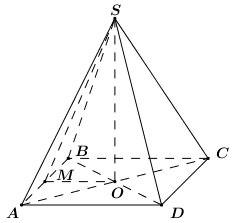
Gọi $O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)$.

Vì $ABCD$ là hình vuông cạnh $a$

$\Rightarrow {S_{ABCD}} = {a^2}$ và $AC = a\sqrt 2$$\Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}$.

${V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}$$\Leftrightarrow \dfrac{{{a^3}}}{{2\sqrt 3 }} = \dfrac{1}{3}.SO.{a^2}$$\Leftrightarrow SO = \dfrac{{a\sqrt 3 }}{2}$.

Gọi $M$ là trung điểm của $AB$.

Tam giác $SAB$ cân tại $S$ suy ra $SM \bot AB$.

$OM$ là đường trung bình của tam giác $ABC$

$\Rightarrow OM\parallel BC \Rightarrow OM \bot AB$ và $OM = \dfrac{1}{2}AB = \dfrac{1}{2}a$.

Ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SM \bot AB\\\left( {ABCD} \right) \supset OM \bot AB\end{array} \right.$$\Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right)$$= \angle SMO$.

Xét tam giác vuông $SOM$ có: $\tan \angle SMO = \dfrac{{SO}}{{OM}}$$= \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 3$.

Vậy $\angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle SMO = {60^0}$.

Chọn C.