Phương pháp giải:

Xác định góc tạo bởi mặt bên và mặt phẳng đáy.

Tính cạnh của tam giác đáy qua thể tích.

Lời giải chi tiết:

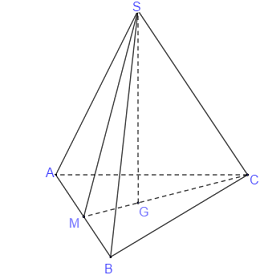
\(S.ABC\) là hình chóp đều nên \(SA = SB = SC\) và \(AB = BC = CA\)

Gọi \(G\) là trọng tâm tam giác \(ABC\). Do \(S.ABC\) là hình chóp đều nên \(G\) là chân đường cao hạ từ \(S\) xuống mặt phẳng \(\left( {ABC} \right)\). Suy ra \(SG = a\)

Gọi \(M\) là trung điểm của \(AB\) thì \(C,G,M\) thẳng hàng và \(CM \bot AB\)

Ta có :

    \(\left. \begin{array}{l}SG \bot \left( {BAC} \right) \Rightarrow SG \bot AB\\CM \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SCM} \right) \Rightarrow AB \bot SM\)

Do đó góc tạo bởi mặt bên và mặt đáy là góc giữa \(SM\) và \(CM\) hay là góc \(\widehat {SMC}\).

Lại có :

     \({V_{S.ABC}} = \sqrt 3 {a^3} \Leftrightarrow \dfrac{1}{3}SG.\dfrac{{\sqrt 3 }}{4}A{B^2} = \sqrt 3 {a^3} \Leftrightarrow \dfrac{{\sqrt 3 }}{{12}}a.A{B^2} = \sqrt 3 {a^3} \Rightarrow AB = 2\sqrt 3 a\)

Tam giác \(ABC\) đều nên \(CM = \dfrac{{\sqrt 3 }}{2}AB = \dfrac{{\sqrt 3 }}{2}.2\sqrt 3 a = 3a \Rightarrow MG = \dfrac{1}{2}CM = a\)

Suy ra \(\tan SMG = \dfrac{{SG}}{{MG}} = \dfrac{a}{a} = 1 \Rightarrow \widehat {SMG} = 45^\circ \)

Vậy góc tạo bởi mặt bên và mặt đáy bằng \(45^\circ \).

Chọn B.