Phương pháp giải:

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến của hai mặt phẳng đó.

Lời giải chi tiết:

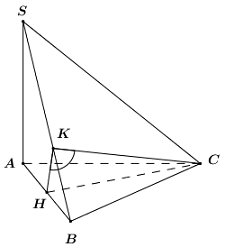
Gọi $H$ là trung điểm của $AB$. Do tam giác $ABC$ đều $\Rightarrow CH \bot AB$.

Mà $CH \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right) \Rightarrow CH \bot \left( {SAB} \right) \Rightarrow CH \bot SB$.

Trong $\left( {SAB} \right)$ kẻ $HK \bot SB$ ta có:

$\left\{ \begin{array}{l}CH \bot SB\\HK \bot SB\end{array} \right. \Rightarrow SB \bot \left( {CHK} \right) \Rightarrow SB \bot CK$.

$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset HK \bot SB\\\left( {SBC} \right) \supset CK \bot SB\end{array} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SBC} \right)} \right) = \angle \left( {HK;CK} \right) = \angle HKC$.

Ta có: $CH \bot \left( {SAB} \right) \Rightarrow CH \bot HK \Rightarrow \Delta CHK$ vuông tại $H$.

Tam giác $ABC$ đều cạnh $a \Rightarrow CH = \dfrac{{a\sqrt 3 }}{2}$.

Dễ thấy $\Delta BHK \sim \Delta BSA\,\,\left( {g.g} \right) \Rightarrow \dfrac{{HK}}{{SA}} = \dfrac{{BH}}{{SB}}$

$\Rightarrow HK = \dfrac{{SA.BH}}{{SB}} = \dfrac{{a\sqrt 3 .\dfrac{a}{2}}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{4}$.

Xét tam giác vuông $CHK$ có:

$\tan \angle HKC = \dfrac{{HC}}{{HK}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{{a\sqrt 3 }}{4}}} = 2 \Rightarrow \cos \angle HKC = \dfrac{1}{{\sqrt {1 + {{\tan }^2}\angle HKC} }} = \dfrac{1}{{\sqrt 5 }}$.

Chọn B