Phương pháp giải:

- Tìm góc tạo bởi hai mặt phẳng \(\left( {ADD'A'} \right)\) và \(\left( {ABCD} \right)\), từ đó tính được độ dài chiều cao \(h\) của lăng trụ đã cho.

- Thể tích của lăng trụ có chiều cao bằng \(h\) và diện tích đáy bằng \(S\) là \(V = Sh\).

Lời giải chi tiết:

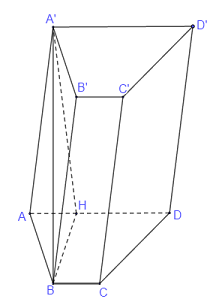
Qua \(B\) kẻ \(BH \bot AD\left( {H \in AD} \right)\)

Ta có :

\(\left. \begin{array}{l}A'B \bot \left( {ABCD} \right) \Rightarrow A'B \bot AD\\BH \bot AD\end{array} \right\} \Rightarrow AD \bot \left( {A'BH} \right) \Rightarrow AD \bot A'H\)

Lại có: \(\left\{ \begin{array}{l}\left( {ADD'A'} \right) \cap \left( {ABCD} \right) = AD\\A'H \bot AD;BH \bot AD\\A'H \subset \left( {ADD'A'} \right);BH \subset \left( {ABCD} \right)\end{array} \right.\).

\( \Rightarrow \widehat {\left( {\left( {ADD'A'} \right),\left( {ABCD} \right)} \right)} = \widehat {A'H,BH} = \widehat {A'HB} = {60^0}\).

\(ABCD\) là hình thang cân nên  \(AH = \dfrac{{AD - BC}}{2} = a\).

Tam giác \(AHB\) vuông tại \(H\) nên \(A{H^2} + B{H^2} = A{B^2} \Leftrightarrow {a^2} + B{H^2} = 2{a^2} \Rightarrow BH = a\)

Tam giác \(A'BH\) vuông tại \(B\) có \(\widehat {A'HB} = 60^\circ ;\,\,BH = a\) nên: \(A'B = BH.\tan A'HB = a.\tan 60^\circ  = \sqrt 3 a\)

Diện tích hình thang \(ABCD\) là: \({S_{ABCD}} = \dfrac{1}{2}BH.\left( {BC + AD} \right) = \dfrac{1}{2}.a.4a = 2{a^2}\).

Vậy thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) là: \({V_{ABCD.A'B'C'D'}} = A'B.{S_{ABCD}} = \sqrt 3 a.2{a^2} = 2\sqrt 3 {a^3}\).

Chọn A.