Phương pháp giải:

+) Trong \(\left( {SBC} \right)\) kẻ \(CF \bot SB\left( {F \in SB} \right)\), trong  \(\left( {SAB} \right)\)kẻ \(GF \bot SB\left( {G \in AB} \right)\)

+) Chứng minh \(\widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {GF;CF} \right)}\)

+) Sử dụng định lí Cosin trong tam giác.

Lời giải chi tiết:

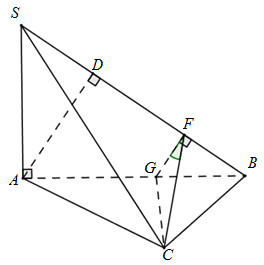
Trong \(\left( {SBC} \right)\) kẻ \(CF \bot SB\left( {F \in SB} \right)\), trong  \(\left( {SAB} \right)\)kẻ \(GF \bot SB\left( {G \in AB} \right)\)

\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\GF \bot SB\\CF \bot SB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {GF;CF} \right)}\)

Ta có: \(SC = \sqrt {S{A^2} + A{C^2}}  = \sqrt {3{a^2} + {a^2}}  = 2a = SB\)

Xét tam giác SBC có: \(cos\widehat {SBC} = \frac{{S{B^2} + B{C^2} - S{C^2}}}{{2.SB.BC}} = \frac{{4{a^2} + {a^2} - 4{a^2}}}{{2.2a.a}} = \frac{1}{4}\)

\(\begin{array}{l} \Rightarrow BF = BC.cos\widehat {SBC} = \frac{1}{4}a\\ \Rightarrow CF = \sqrt {B{C^2} - B{F^2}}  = \sqrt {{a^2} - \frac{1}{{16}}{a^2}}  = \frac{{a\sqrt {15} }}{4}\end{array}\)

Ta có:

\(\begin{array}{l}\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow GF = BF.tan\widehat {SBA} = \frac{{\sqrt 3 }}{4}a \Rightarrow BG = \sqrt {B{F^2} + G{F^2}}  = \sqrt {\frac{{{a^2}}}{{16}} + \frac{{3{a^2}}}{{16}}}  = \frac{a}{2}\end{array}\)

\( \Rightarrow \)G là trung điểm của AB \( \Rightarrow GC = \frac{{a\sqrt 3 }}{2}\)

\( \Rightarrow cos\widehat {CFG} = \dfrac{{G{F^2} + C{F^2} - G{C^2}}}{{2.GF.CF}} = \dfrac{{\dfrac{{3{a^2}}}{{16}} + \dfrac{{15{a^2}}}{{16}} - \dfrac{{3{a^2}}}{4}}}{{2.\dfrac{{a\sqrt 3 }}{4}.\dfrac{{a\sqrt {15} }}{4}}} = \dfrac{{\dfrac{3}{8}{a^2}}}{{\dfrac{{3\sqrt 5 {a^2}}}{8}}} = \dfrac{1}{{\sqrt 5 }}\)

Chọn D.