Phương pháp giải:

+) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)

+) Trong $\left( {SAE} \right)$ kẻ $DF \bot SE$

+) Chứng minh DF và BF cùng vuông góc với giao tuyến.

Lời giải chi tiết:

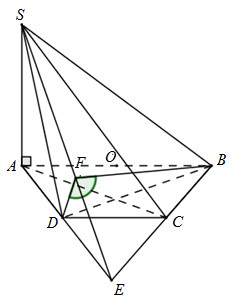
Gọi $E = AD \cap BC$
Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB
nên $\widehat {ADB} = {90^0} \Rightarrow AD \bot DB$
Mà $SA \bot DB$
$\Rightarrow DB \bot \left( {SAD} \right) \Rightarrow DB \bot SE$
Trong $\left( {SAE} \right)$ kẻ $DF \bot SE$
$\Rightarrow SE \bot \left( {BDF} \right) \Rightarrow SE \bot BF$
Ta có: $\left. \begin{array}{l}\left( {SAD} \right) \cap \left( {SBC} \right) = SE\\DF \bot SE\\BF \bot SE\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAD} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {DF;BF} \right)} = \widehat {BFD}$

(vì $\widehat {BFD} < {90^0}$)

Vì $DB \bot \left( {SAD} \right) \Rightarrow DB \bot DF \Rightarrow \Delta BDF$vuông tại D

Xét tam giác vuông ABD có: $BD = \sqrt {A{B^2} - A{D^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3$

$\Delta EAB$ đều nên $AE = BE = AB = 2a \Rightarrow SE = \sqrt {S{A^2} + A{E^2}}  = \sqrt {3{a^2} + 4{a^2}}  = a\sqrt 7$

D là trung điểm của AE nên $AD = \frac{1}{2}AE = a$

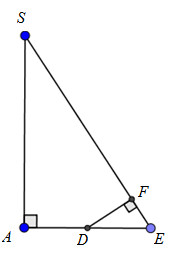
Ta có: $\Delta EDF \sim \Delta ESA\left( {g.g} \right) \Rightarrow \dfrac{{DF}}{{SA}} = \dfrac{{DE}}{{SE}} \Rightarrow DF = \dfrac{{SA.DE}}{{SE}} = \dfrac{{a\sqrt 3 .a}}{{a\sqrt 7 }} = \dfrac{{a\sqrt 3 }}{{\sqrt 7 }}$

$\Rightarrow BF = \sqrt {D{F^2} + B{D^2}}  = \sqrt {\dfrac{3}{7}{a^2} + 3{a^2} = } \dfrac{{2\sqrt 6 a}}{{\sqrt 7 }}$

Vậy $cos\widehat {BFD} = \dfrac{{DF}}{{BF}} = \dfrac{{\dfrac{{a\sqrt 3 }}{{\sqrt 7 }}}}{{\dfrac{{2\sqrt 6 a}}{{\sqrt 7 }}}} = \dfrac{{\sqrt 2 }}{4}$

Chọn C.