Câu hỏi:
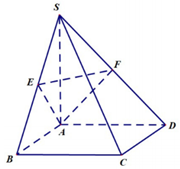
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh a, SA vuông góc với \(\left( {ABCD} \right)\), \(SA = a\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(SB\) và \(SD\). Côsin của góc hợp bởi hai mặt phẳng \(\left( {AEF} \right)\) và \(\left( {ABCD} \right)\) là:
- A \(\sqrt 3 \).
- B \(\frac{1}{2}\).
- C \(\frac{{\sqrt 3 }}{3}\).
- D \(\frac{{\sqrt 3 }}{2}\).
Phương pháp giải:
\(\cos \left( {\widehat {\left( P \right);\left( Q \right)}} \right) = \frac{{S'}}{S}\).
Lời giải chi tiết:
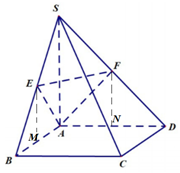
Gọi M, N lần lượt là hình chiếu của E, F lên (ABCD). Ta có: \({S_{\Delta AMN}} = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
\(AE = AF = EF = \frac{{a\sqrt 2 }}{2} \Rightarrow {S_{\Delta AEF}} = \frac{{{a^2}\sqrt 3 }}{8}\)\( \Rightarrow \cos \left( {\widehat {\left( {AEF} \right);\left( {ABCD} \right)}} \right) = \frac{{{S_{\Delta AMN}}}}{{{S_{\Delta AEF}}}} = \frac{{\sqrt 3 }}{3}\).
Chọn: C