Phương pháp giải:

$\left( {DMN} \right),\left( {ABC} \right)$ vuông góc với nhau $\Rightarrow \left( {DMN} \right)$ luôn đi qua đường cố định là đường vuông góc kẻ từ D đến (ABC). Bài toán: Cho G là trọng tâm tam giác ABC, đường thẳng qua G cắt cạnh AB, AC lần lượt tại M, N. Ta chứng minh được: $\dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = 3$. Thật vậy, Gọi I, J, K lần lượt là trung điểm của AB, BC, AC.

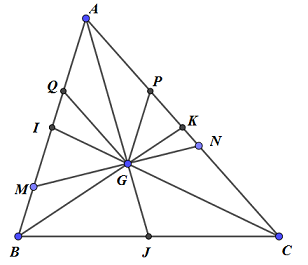
Dựng GP // AB, GQ // AC, $\left( {P \in AC,\,\,Q \in AB} \right)$.

Ta có: $\dfrac{{GP}}{{AB}} = \dfrac{{GK}}{{BK}} = \dfrac{1}{3},\,\,\dfrac{{GQ}}{{AC}} = \dfrac{{GI}}{{IC}} = \dfrac{1}{3}$

Lại có: $\dfrac{{GP}}{{AM}} = \dfrac{{GN}}{{MN}},\,\,\,\,\dfrac{{GQ}}{{AN}} = \dfrac{{GM}}{{MN}}$

$\Rightarrow \dfrac{{AB}}{{AM}} = 3.\dfrac{{GN}}{{MN}},\,\,\dfrac{{AC}}{{AN}} = 3.\dfrac{{GM}}{{MN}} \Rightarrow \dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = 3$ (đpcm).

Lời giải chi tiết:

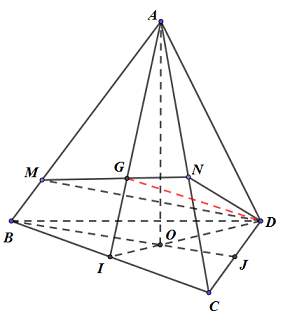
Gọi G là tâm của tam giác đều ABC. Do $ABCD$ là tứ diện đều nên $DG \bot \left( {ABC} \right)$

Ta có: $\left( {DMN} \right) \bot \left( {ABC} \right) \Rightarrow \left( {DMN} \right) \supset DG \Rightarrow G \in MN$

Áp dụng bài toán đã chứng minh ở trên, ta có:

$\dfrac{{AB}}{{AM}} + \dfrac{{AC}}{{AN}} = 3 \Leftrightarrow \dfrac{1}{x} + \dfrac{1}{y} = 3 \Leftrightarrow x + y = 3xy$.

Chọn: B