Bài 9 trang 29 SGK Hình học 10

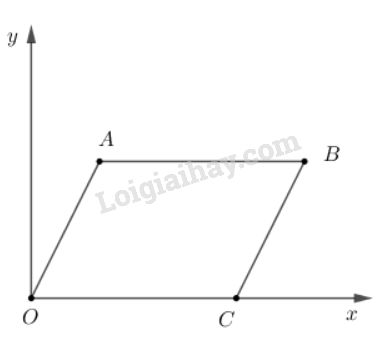
Đề bài

Trong mặt phẳng tọa độ $Oxy$ cho hình bình hành $OABC$, $C$ nằm trên $Ox$.

Khẳng định nào sau đây là đúng?

A. $\overrightarrow {AB}$ có tung độ khác $0$

B. $A$ và $B$ có tung độ khác nhau

C. $C$ có hoành độ bằng $0$

D. ${x_A} + {x_C} - {x_B} = 0$

Lời giải chi tiết

Trong mặt phẳng tọa độ $O xy$, hình bình hành $OABC$ có $C$ nằm trên $Ox$ nên điểm $C({x_c};0)$

$\overrightarrow {AB}  = \overrightarrow {OC}$$=(x_C-0;0-0)=(x_C;0)$

Do đó $\overrightarrow {AB}$ có tung độ bằng 0 nên A sai.

$\overrightarrow {AB}$ có tung độ bằng 0 nên $y_B-y_A=0$ hay $y_B=y_A$ nên B sai.

C sai vì C không trùng O nên $x_C\ne 0$.

D đúng vì:

Từ $\overrightarrow {AB}  = \overrightarrow {OC}$ $\Rightarrow {x_B} - {x_A} = {x_C}-x_O$ $\Leftrightarrow {x_A} + {x_C} - {x_B} = 0$

Chọn D.

Loigiaihay.com