Câu 88 trang 131 Sách bài tập Hình học 11 Nâng cao

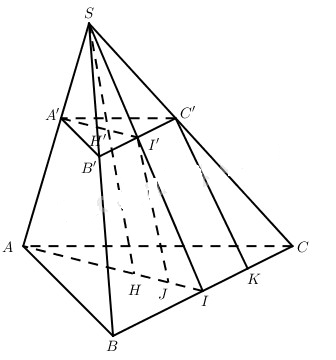
Đề bài

Cho hình chóp cụt tam giác đều ABC.A’B’C’ có các cạnh đáy lần lượt là a, b (a>b). Góc giữa đường thẳng chứa đường cao và mặt phẳng chứa mặt bên là α. Tính:

a) Chiều cao, trung đoạn, cạnh bên của hình chóp cụt đó (đoạn thẳng nối trung điểm hai cạnh đáy thuộc một mặt bên gọi trung đoạn của hình chóp cụt đều).

b) Diện tích xung quanh, diện tích toàn phần của hình chóp cụt đó.

Lời giải chi tiết

a) Gọi S là đỉnh của hình chóp đều sinh ra hình chóp cụt đều A’B’C’.ABCD; các điểm H, H’ lần lượt là tâm hai đáy của hình chóp cụt đều; I là trung điểm của BC. Dễ thất \(\widehat {H{\rm{S}}I} = \alpha \), từ đó \(\widehat {SIH} = {90^0} - \alpha  = \beta \).

Ta có \(HH' = I'J = JI.\tan \beta  = JI.\cot \alpha \)

Mà \(JI = {{a\sqrt 3 } \over 6} - {{b\sqrt 3 } \over 6} = {{\sqrt 3 } \over 6}\left( {a - b} \right)\)

Vậy

\(\eqalign{  & HH' = {{\sqrt 3 } \over 6}\left( {a - b} \right)\cot \alpha   \cr  & II' = {{JI} \over {\cos \beta }} = {{JI} \over {\sin \alpha }} = {{\sqrt 3 \left( {a - b} \right)} \over {6\sin \alpha }}  \cr  & CC{'^2} = C'{K^2} + K{C^2}  \cr  &  = {\left( {{{\sqrt 3 \left( {a - b} \right)} \over {6\sin \alpha }}} \right)^2} + {\left( {{{a - b} \over 2}} \right)^2}  \cr  &  \Rightarrow CC' = {{a - b} \over {2\sqrt 3 \sin \alpha }}\sqrt {1 + 3{{\sin }^2}\alpha }  \cr} \)

b)

\(\eqalign{  & {S_{xq}} = 3.{1 \over 2}\left( {B'C' + BC} \right).II'  \cr  &  = {3 \over 2}\left( {a + b} \right){{\sqrt 3 \left( {a - b} \right)} \over {6\sin \alpha }} = {{\sqrt 3 } \over {4\sin \alpha }}\left( {{a^2} - {b^2}} \right)  \cr  & {S_{tp}} = {{\sqrt 3 } \over {4\sin \alpha }}\left( {{a^2} - {b^2}} \right) + {{\sqrt 3 } \over 4}\left( {{a^2} + {b^2}} \right)  \cr  &  = {{\sqrt 3 } \over 4}\left( {{{{a^2} - {b^2}} \over {\sin \alpha }} + {a^2} + {b^2}} \right) \cr} \).

Loigiaihay.com