Câu 81 trang 129 Sách bài tập Hình học 11 Nâng cao

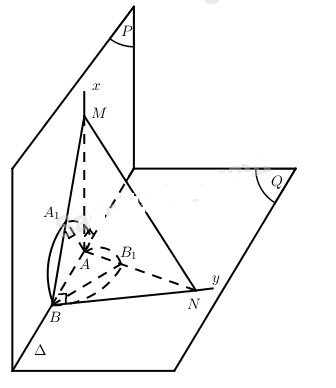
Đề bài

Cho hai nửa mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến ∆. Trên ∆ lấy hai điểm A, B cố định với \(AB = a\sqrt 2 \) (a là độ dài cho trước). Trên nửa đường thẳng Ax vuông góc với ∆ và ở trong (P) lấy điểm M khác A. Đặt AM = m. Trên nửa đường thẳng By vuông góc với ∆ và trong (Q) lấy điểm N sao cho \(BN = {{{a^2}} \over m}\).

a) Chứng minh các mặt của tứ diện ABMN là các tam giác vuông.

b) Với giá trị nào của m thì MN có độ dài bé nhất? Tính giá trị đó.

c) Chứng minh rằng chân mỗi đường cao của tứ diện đó xuất phát từ A và B nằm trên đường tròn cố định khi M thay đổi.

Lời giải chi tiết

a) Vì \(\left( P \right) \bot \left( Q \right),\left( P \right) \cap \left( Q \right) = AB,\)

\(M \in \left( P \right),MA \bot AB\) nên \(MA \bot \left( Q \right)\). Do đó MAB, MAN là các tam giác vuông tại A.

Tương tự như trên, các tam giác MBN, ABN vuông tại B.

b) Vì

\(\eqalign{  & M{N^2} = M{A^2} + A{B^2} + B{N^2}  \cr  &  = {m^2} + 2{a^2} + {{{a^4}} \over {{m^2}}} \cr} \)

Từ đó MN có độ dài bé nhất khi và chỉ khi \({m^2} + {{{a^4}} \over {{m^2}}}\) bé nhất.

Mặt khác \({m^2}.{{{a^4}} \over {{m^2}}} = {a^4}\).

Vậy MN có độ dài bé nhất khi và chỉ khi:

\({m^2} = {{{a^4}} \over {{m^2}}} \Leftrightarrow m = a\).

c) Vì \(\left( {MAB} \right) \bot \left( {NMB} \right)\) nên khi kẻ AA₁ vuông góc với BM tại A₁ thì \(A{A_1} \bot \left( {BMN} \right)\), tức A­₁ là chân đường cao của tứ diện ABMN kẻ từ đỉnh A.

Như vậy A₁ thuộc (P) và \(\widehat {B{A_1}A} = {90^0}\), từ đó A₁ thuộc đường tròn đường kính AB trong (P). Đường tròn này cố định.

Tương tự như trên, chân đường cao B_1­ kẻ từ đỉnh B của tứ diện ABMN cũng thuộc đường tròn đường kính AB nằm trong mặt phẳng (Q).

Loigiaihay.com