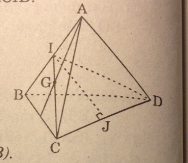
Câu 8 trang 80 SGK Hình học 11 Nâng caoCho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là : Quảng cáo
Đề bài Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là : A. \({{{a^2}\sqrt 3 } \over 2}\) B. \({{{a^2}\sqrt 2 } \over 4}\) C. \({{{a^2}\sqrt 2 } \over 6}\) D. \({{{a^2}\sqrt 3 } \over 4}\) Lời giải chi tiết
Gọi I là trung điểm của AB. Thiết diện cần tìm là ΔCID Gọi J là trung điểm CD ΔCID cân nên IJ ⊥ CD ⇒ \({S_{ICD}} = {1 \over 2}IJ.CD\) Ta có: \(\eqalign{ & I{J^2} = C{I^2} - C{J^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \cr & \Rightarrow IJ = {{a\sqrt 2 } \over 2} \Rightarrow {S_{ICD}} = {1 \over 2}.{{a\sqrt 2 } \over 2}.a = {{{a^2}\sqrt 2 } \over 4} \cr} \) Chọn (B) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
