Câu 62 trang 126 Sách bài tập Hình học 11 Nâng cao

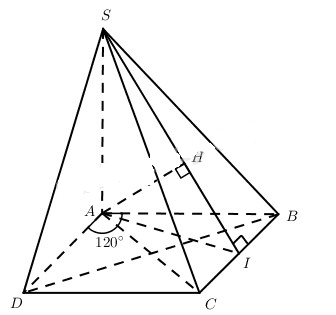
Đề bài

Cho hình chóp S.ABCD có đáy là hình thoi. \(\widehat A = {120^0},B{\rm{D}} = a\), cạnh bên SA vuông góc với đáy, góc giữa mặt phẳng (SBC) và mặt phẳng đáy là 60°. Tính:

a) Đường cao của hình chóp.

b) Khoảng cách từ A đến mặt phẳng (SCB).

Lời giải chi tiết

a) Vì ABCD là hình thoi và \(\widehat {BA{\rm{D}}} = {120^0}\) nên ABC là tam giác đều. Gọi I là trung điểm của BC thì \(BC \bot \left( {AIS} \right)\).

Mặt khác SAI là tam giác vuông tại A nên \(\widehat {SIA}\) là góc giữa hai mặt phẳng (SBC) và mặt phẳng đáy (ABCD). Theo giả thiết \(\widehat {SIA} = {60^0}\).

Ta có \(B{{\rm{D}}^2} + A{C^2} = 4{\rm{A}}{B^2}\).

mà AC = AB nên

\(AB = {{B{\rm{D}}} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} \Rightarrow AI = {a \over {\sqrt 3 }}.{{\sqrt 3 } \over 2} = {a \over 2}\).

Vì \(SA \bot \left( {ABC{\rm{D}}} \right)\) nên SA là đường cao của hình chóp S.ABCD. Ta có :

\(SA = AI.\tan {60^0}\).

Vậy  \(SA = {a \over 2}\sqrt 3 \).

b) Ta có \(BC \bot \left( {SAI} \right)\), từ đó \(\left( {SAI} \right) \bot \left( {SBC} \right)\). Vậy nếu kẻ đường cao AH của tam giác SAI thì AH là khoảng cách từ A đến mp(SBC). Xét tam giác vuông SAI ta có:

\(AH = {{SA.AI} \over {SI}} = {{{{a\sqrt 3 } \over 2}.{a \over 2}} \over {\sqrt {{{3{{\rm{a}}^2}} \over 4} + {{{a^2}} \over 4}} }} = {{a\sqrt 3 } \over 4}.\)

Vậy khoảng cách từ A đến mặt phẳng (SCB) bằng \({{a\sqrt 3 } \over 4}\).

Loigiaihay.com