Câu 67 trang 127 Sách bài tập Hình học 11 Nâng cao

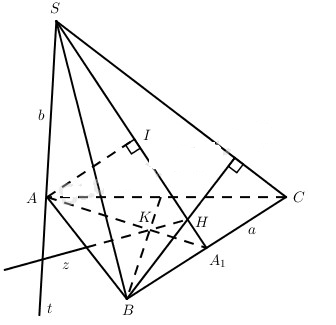
Đề bài

Cho ABC là tam giác đều cạnh a. Trên đường thẳng At vuông góc với mp(ABC) lấy điểm S với AS = b.

a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, b.

b) Hz là đường thẳng đi qua trực tâm H của tam giác SBC và vuông góc với mp(SBC). Chứng minh rằng khi S di động trên At thì đường thẳng Hz luôn đi qua một điểm cố định.

Lời giải chi tiết

a) Gọi A₁ là trung điểm của BC thì \(BC \bot mp\left( {SA{A_1}} \right)\),  từ đó \(\left( {SA{A_1}} \right) \bot \left( {SBC} \right)\).

Kẻ đường cao AI của tam giác SAA₁ thì \(AI \bot \left( {SBC} \right)\). Từ đó, khoảng cách từ A đến mp(SBC) bằng AI.

Ta có \(AI = {{AS.A{A_1}} \over {S{A_1}}} = {{b.{{a\sqrt 3 } \over 2}} \over {\sqrt {{b^2} + {{3{a^2}} \over 4}} }}\).

Vậy \(AI = {{ab\sqrt 3 } \over {\sqrt {3{{\rm{a}}^2} + 4{b^2}} }}\).

b) Vì H là trực tâm tam giác SBC nên H thuộc SA₁. Do \(\left( {SA{A_1}} \right) \bot \left( {SBC} \right)\)  và \(H{\rm{z}} \bot \left( {SBC} \right)\) nên Hz nằm trong mp(SAA₁). Gọi K là giao điểm của Hz và AA₁, ta có \(KH \bot \left( {SBC} \right),BH \bot SC\) nên \(KB \bot SC\) (định lí ba đường vuông góc).

Mặt khác \(SA \bot \left( {ABC} \right),BK \bot SC\) nên \(BK \bot AC\) (định lí ba đường vuông góc). Như vậy K là trực tâm của tam giác ABC.

Vậy khi S di động trên đường thẳng At vuông góc với mp(ABC) thì đường thẳng Hz đi qua điểm cố định là trực tâm K của tam giác ABC.

Loigiaihay.com