Câu 55 trang 124 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi C₁ là trung điểm của CC’.

a) Tính góc giữa hai đường thẳng C₁B và A’B’. Tính góc giữa hai mặt phẳng (C₁AB) và (ABC).

b) Chứng minh rằng hình chóp C₁.ABB’A’ là hình chóp tứ giác đều.

c) Một mặt phẳng (P) chứa cạnh AB, tạo với mặt phẳng đáy (ABC) góc φ và cắt hình lăng trụ đã cho theo hình có diện tích khác không. Tính diện tích thiết diện đó theo a và φ.

Lời giải chi tiết

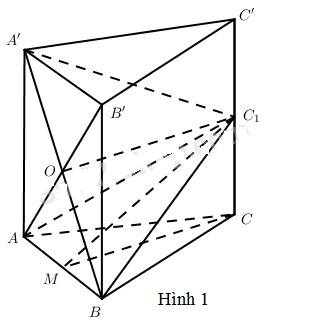
a) (Hình 1) Vì AB // A’B’ nên góc giữa C₁B và A’B’ là góc giữa C₁B và AB. Dễ thấy AC₁ = BC₁ nên AC₁B là tam giác cân. Từ đó \(\widehat {AB{C_1}} < {90^0}\). Vậy góc giữa AB và AC₁ là \(\widehat {AB{C_1}}\). Gọi M là trung điểm của AB thì:

\(MB = {a \over 2},B{C_1} = {{a\sqrt 5 } \over 2},MB \bot M{C_1}\).

Từ đó \(\cos \widehat {{C_1}BA} = {{MB} \over {{C_1}B}} = {1 \over {\sqrt 5 }}\).

Cũng từ kết quả trên, ta có \(\left( {{C_1}MC} \right) \bot AB\) và C₁MC là tam giác vuông tại C nên góc giữa mp(C₁AB) và (CAB) là \(\widehat {{C_1}MC}\).

Ta có \(\tan \widehat {{C_1}MC} = {{{C_1}C} \over {MC}} = {{{a \over 2}} \over {{{a\sqrt 3 } \over 2}}} = {1 \over {\sqrt 3 }}\).

Vậy \(\widehat {{C_1}MC} = {30^0}\) hay góc giữa mp(C₁AB) và mp(ABC) bằng 30°.

b) ABB’A’ là hình vuông. Dễ thấy \({C_1}A = {C_1}B = {C_1}A' = {C_1}B' = {{a\sqrt 5 } \over 2}\).

Khi đó \({C_1}O \bot AB',{C_1}O \bot A'B\left( {O = A'B \cap AB'} \right)\).

Vậy C₁.ABB’A’ là hình chóp tứ giác đều.

c) Trong mp(M, CC’) kẻ tia Mt sao cho \(\widehat {CMt} = \varphi \) thì mp(AB, Mt) chính là mặt phẳng (P) phải tìm.

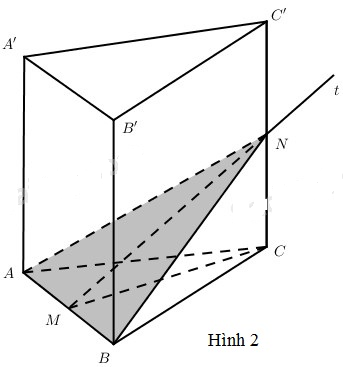
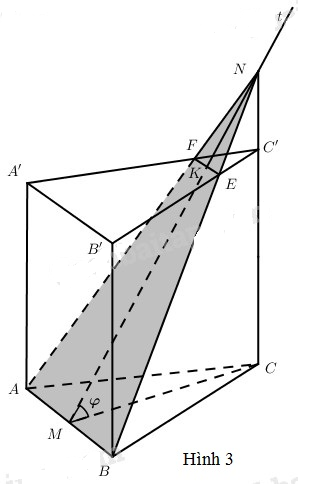
- Nếu \({0^0} \le \varphi  \le \widehat {C'MC}\) thì thiết diện là tam giác ABN (Hình 2)

Khi đó:

\(\eqalign{  & {S_{ABN}} = {1 \over 2}AB.MN  \cr  & AB = a,MN = {{MC} \over {\cos \varphi }} = {{a\sqrt 3 } \over {2\cos \varphi }} \cr} \)

Vậy \({S_{ABN}} = {{{a^2}\sqrt 3 } \over {4\cos \varphi }}\)

- Nếu \(\widehat {C'MC} < \varphi  < {90^0}\) thì thiết diện là hình thang cân ABEF (Hình 3).

Khi đó \({S_{ABEF}} = {S_{ABN}} - {S_{EFN}}\).

Ta có

\(\eqalign{  & {S_{ABN}} = {{{a^2}\sqrt 3 } \over {4\cos \varphi }}  \cr  & {{{S_{EFN}}} \over {{S_{ABN}}}} = {\left( {{{NE} \over {NB}}} \right)^2} = {\left( {{{NC'} \over {NC}}} \right)^2}  \cr  &  = {{{{\left( {{{a\sqrt 3 } \over 2}\tan \varphi  - a} \right)}^2}} \over {{{\left( {{{a\sqrt 3 } \over 2}\tan \varphi } \right)}^2}}} = {{{{\left( {\sqrt 3 \tan \varphi  - 2} \right)}^2}} \over {3{{\tan }^2}\varphi }} \cr} \)

Vậy \({S_{EFN}} = {{{a^2}\sqrt 3 } \over {4\cos \varphi }}.{{{{\left( {\sqrt 3 \tan \varphi  - 2} \right)}^2}} \over {3{{\tan }^2}\varphi }}\)

Từ đó

\(\eqalign{  & {S_{ABEF}} = {{{a^2}\sqrt 3 } \over {4.\cos \varphi }}.\left[ {1 - {{{{\left( {\sqrt 3 \tan \varphi  - 2} \right)}^2}} \over {3{{\tan }^2}\varphi }}} \right]  \cr  &  = {{{a^2}\sqrt 3 } \over {12{{\tan }^2}\varphi \cos \varphi }}.\left( {4\sqrt 3 \tan \varphi  - 4} \right)  \cr  &  = {{{a^2}\sqrt 3 } \over {3\tan \varphi .\sin \varphi }}\left( {\sqrt 3 \tan \varphi  - 1} \right) \cr} \)

- Nếu \(\varphi  = {90^0}\) thì thiết diện là hình vuông ABB’A’. Khi đó diện tích thiết diện bằng a².

Loigiaihay.com