Câu 5 trang 9 SGK Hình học 11 Nâng caoTrong mặt phẳng tọa độ , Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Trong mặt phẳng tọa độ Oxy , với \(\alpha ,a,b\)là những số cho trước, xét phép biến hình F biến mỗi điểm \(M\left( {x;y} \right)\) thành điểm \(M'\left( {x';y'} \right)\), trong đó \(\left\{ {\matrix{{x' = x\cos \alpha - y\sin \alpha + a} \cr {y' = x\sin \alpha + y\cos \alpha + b} \cr} } \right.\) LG a Cho hai điểm \(M\left( {{x_1};{y_1}} \right),\,N\left( {{x_2};{y_2}} \right)\) và gọi M', N' lần lượt là ảnh của M,N qua phép F. Hãy tìm tọa độ của M' và N'. Lời giải chi tiết: M’ có tọa độ \({(x_1'},{\rm{ }}y{_1}')\) với \(\left\{ {\matrix{{x{'_1} = {x_1}\cos \alpha - {y_1}\sin \alpha + a} \cr {y{'_1} = {x_1}\sin \alpha + {y_1}\cos \alpha + b} \cr} } \right.\) N’ có tọa độ \({(x_2'},{\rm{ }}y{_2}')\) với \(\left\{ {\matrix{{x{'_2} = {x_2}\cos \alpha - {y_2}\sin \alpha + a} \cr {y{'_2} = {x_2}\sin \alpha + {y_2}\cos \alpha + b} \cr} } \right.\) LG b Tính khoảng cách d giữa M và N; khoảng cách d' giữa M' và N' Lời giải chi tiết: Ta có \(d=MN=\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)
LG c Phép F có phải là phép dời hình hay không ? Lời giải chi tiết: Từ câu b suy ra \(MN=M'N'\) do đó \(F\) là phép dời hình. LG d Khi \(\alpha = 0\), chứng tỏ rằng F là phép tịnh tiến Lời giải chi tiết: Khi \(\alpha=0\) thì: \(\begin{array}{l} Vậy \(F\) là phép tịnh tiến vectơ \(\overrightarrow u \left( {a;b} \right).\) Loigiaihay.com
|














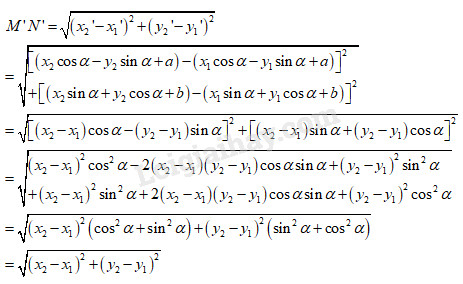






Danh sách bình luận