Câu 47 trang 59 - 60 Sách Bài tập Hình học 11 Nâng caoCho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AB và CD. Một mặt phẳng IJ cắt các cạnh AD và BC lần lượt tại N và M. Quảng cáo
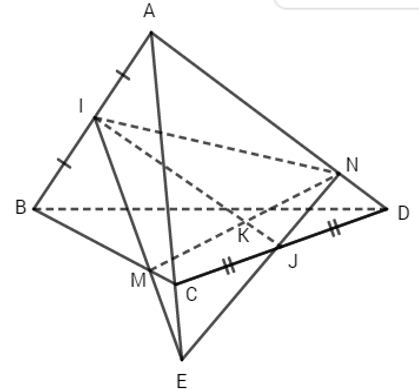
Đề bài Cho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AB và CD. Một mặt phẳng IJ cắt các cạnh AD và BC lần lượt tại N và M. a) Cho trước điểm M, nêu cách dựng điểm N. b) Gọi K là giao điểm của MN và IJ. Chứng minh rằng K là trung điểm của MN. Lời giải chi tiết (h.100)
a) Trường hợp M không phải là trung điểm của BC Nối M với I cắt AC tại E. Nối E với J cắt AD tại N, N chính là điểm cần tìm Trường hợp M là trung điểm của BC. Khi đó IM // AC và (IJM) // AC. Vậy mp(IJM) cắt mp(ACD) theo giao tuyến JN // AC. b) Vì \({{IA} \over {JD}} = {{IB} \over {JC}} = {{AB} \over {DC}}\), nên qua IJ, AD, BC có ba mặt phẳng song song (định lí Ta-lét đảo). Ba mặt phẳng này cắt hai đường thẳng AB và NM tại các điểm I, A, B và K, N, M. Vì I là trung điểm của AB nên K là trung điểm của MN (định lí Ta-lét). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
