Câu 45 trang 122 Sách bài tập Hình học 11 Nâng cao

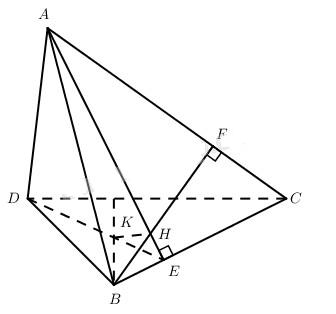
Đề bài

Cho tứ diện ABCD có cạnh AD vuông góc với mp(DBC). Gọi AE, BF là hai đường cao của tam giác ABC; H và K lần lượt là trực tâm của tam giác ABC và tam giác DBC. Chứng minh rằng:

a) \(mp\left( {A{\rm{D}}E} \right) \bot mp\left( {ABC} \right)\) và \(mp\left( {BFK} \right) \bot mp\left( {ABC} \right)\).

b) \(HK \bot mp\left( {ABC} \right)\)

Lời giải chi tiết

a) Vì \(A{\rm{D}} \bot \left( {DBC} \right)\) nên \(A{\rm{D}} \bot BC\).

Mặt khác \(A{\rm{E}} \bot BC\). Vậy \(BC \bot \left( {A{\rm{D}}E} \right)\), từ đó ta có \(\left( {ABC} \right) \bot \left( {A{\rm{D}}E} \right)\).

Vì K là trực tâm tam giác DBC nên \(BK \bot AC\). Theo giả thiết \(A{\rm{D}} \bot \left( {DBC} \right)\), vậy \(BK \bot AC\) (định lí ba đường vuông góc). Kết hợp với \(BF \bot AC\) ta có \(AC \bot \left( {BFK} \right)\), từ đó \(mp\left( {ABC} \right) \bot mp\left( {BFK} \right)\).

b) Từ câu a), ta có

\(\eqalign{  & mp\left( {BFK} \right) \bot mp\left( {ABC} \right)  \cr  & mp\left( {A{\rm{D}}E} \right) \bot mp\left( {ABC} \right)  \cr  & HK = mp\left( {A{\rm{D}}E} \right) \cap mp\left( {BFK} \right) \cr} \)

Vậy \(HK \bot mp\left( {ABC} \right)\).

Loigiaihay.com