Câu 31 trang 41 SGK Đại số và Giải tích 11 Nâng cao

Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí cân bằng

Quảng cáo

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

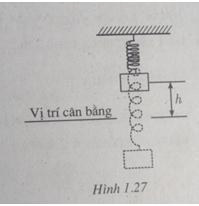
Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí cân bằng.

Khoảng cách \(h\) từ vật đó đến vị trí cân bằng ở thời điểm \(t\) giây được tính theo công thức \(h = |d|\) trong đó

\(d = 5\sin6t – 4\cos6t\),

với \(d\) được tính bằng xentimet, ta quy ước rằng \(d > 0\) khi vật ở phía trên vị trí cân bằng, \(d < 0\) khi vật ở phía dưới vị trí cân bằng. Hỏi :

LG a

Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng ?

Lời giải chi tiết:

Ta có:\(d=5\sin 6t - 4cos6t\) \( = \sqrt {41} \left( {{5 \over {\sqrt {41} }}\sin 6t - {4 \over {\sqrt {41} }}\cos 6t} \right) \) \(= \sqrt {41} \sin \left( {6t - \alpha } \right)\)

trong đó số \(α\) được chọn sao cho \(\cos \alpha = {5 \over {\sqrt {41} }}\,\text{ và }\,\sin \alpha = {4 \over {\sqrt {41} .}}\)

Sử dụng bảng số hoặc máy tính bỏ túi, ta chọn được \(α ≈ 0,675\).

Vật ở vị trí cân bằng khi \(d = 0\), nghĩa là \(\sin(6t – α) = 0\)

\( \Leftrightarrow t = {\alpha \over 6} + k{\pi \over 6}\) (với \(k \in\mathbb Z\))

Ta cần tìm \(k\) nguyên dương sao cho \(0 ≤ t ≤ 1\)

\(0 ≤ t ≤ 1\) \( ⇔ 0 \le {\alpha \over 6} + k{\pi \over 6} \le 1 \) \(\Leftrightarrow - {\alpha \over \pi } \le k \le {{6 - \alpha } \over \pi }\)

Với \(α ≈ 0,675\), ta thu được \(-0,215 < k < 1,7\), nghĩa là \(k\in \{0;1\}\).

Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở vị trí cân bằng là :

\(t \approx {\alpha \over 6} \approx 0,11\) (giây) và \(t = {\alpha \over 6} + {\pi \over 6} \approx 0,64\) (giây)

LG b

Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất ?

(Tính chính xác đến \({1 \over {100}}\) giây).

Lời giải chi tiết:

Vật ở xa vị trí cân bằng nhất khi và chỉ khi \(|d|\) nhận giá trị lớn nhất.

Điều đó xảy ra nếu \(\sin(6t – α) = ± 1\). Ta có :

\(\sin \left( {6t - \alpha } \right) = \pm 1 \)

\(\Leftrightarrow \cos \left( {6t - \alpha } \right) = 0 \)

\(\Leftrightarrow t= {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6}\)

Ta tìm k nguyên dương sao cho \(0 ≤ t ≤ 1\)

\(\eqalign{
& 0 \le t \le 1 \Leftrightarrow 0 \le {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6} \le 1 \cr
& \Leftrightarrow - {\alpha \over \pi } - {1 \over 2} \le k \le {{6 - \alpha } \over \pi } - {1 \over 2} \cr} \)

Với \(α ≈ 0,675\), ta thu được \(-0,715 < k < 1,2\); nghĩa là \(k \in {\rm{\{ }}0;1\} \). Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất là :

\(t = {\alpha \over 6} + {\pi \over {12}} \approx 0,37\,\left( {s} \right)\) và \(t = {\alpha \over 6} + {\pi \over {12}} + {\pi \over 6} \approx 0,90\,\left( \text{s} \right)\)

Loigiaihay.com