Câu 30 trang 117 SGK Hình học 11 Nâng cao

Đề bài

Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.

a. Tính khoảng cách giữa hai mặt phẳng đáy

b. Chứng minh rằng hai đường thẳng AA’ và B’C’ vuông góc, tính khoảng cách giữa chúng.

Lời giải chi tiết

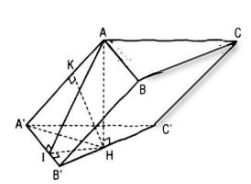
Ta có: AH ⊥ (A’B’C’) nên \(\widehat {AA'H}\) là góc giữa AA’ và mp(A’B’C’) do đó \(\widehat {AA'H} = 30^\circ \)

a. Khoảng cách giữa hai mp đáy chính là AH, ta có :

\(AH = AA'\sin 30^\circ  = {a \over 2}\)

b. Tam giác AHA’ vuông tại H nên \(A'H = AA'\cos 30^\circ  = {{a\sqrt 3 } \over 2}.\) Vì A’B’C’ là tam giác đều cạnh a, H thuộc đường thẳng B’C’ mà \(A'H = {{a\sqrt 3 } \over 2}\) nên A’H ⊥ B’C’ và H là trung điểm B’C’.

Mặt khác, AH ⊥ B’C’ nên AA’ ⊥ B’C’. Kẻ đường cao HK của tam giác AA’H thì HK chính là khoảng cách giữa AA’ và B’C’. Do AA’.HK = AH.A’H nên \(HK = {{{a \over 2}.{{a\sqrt 3 } \over 2}} \over a} = {{a\sqrt 3 } \over 4}\)

Loigiaihay.com