Bài 3 trang 99 SGK Hình học 10

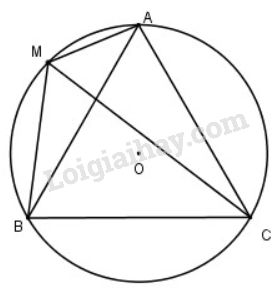
LG a

Cho $M$ là một điểm trên đường tròn ngoại tiếp tam giác $ABC$. Tính $MA^2+ MB^2+ MC^2$ theo $a$

Lời giải chi tiết:

Ta có:

$\eqalign{ & \overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} \cr  & {\overrightarrow {MA} ^2} = {(\overrightarrow {OA} - \overrightarrow {OM} )^2}\cr&\;\;\;\;\;\;\;\;\;\, = {\overrightarrow {OA} ^2} + {\overrightarrow {OM} ^2} - 2\overrightarrow {OA} .\overrightarrow {OM} \cr  & \Rightarrow {\overrightarrow {MA} ^2} = 2{R^2} - 2\overrightarrow {OA} .\overrightarrow {OM} (1) \cr}$

Tương tự ta có:

$\eqalign{ & M{B^2} = {\overrightarrow {MB} ^2} = 2{R^2} - 2\overrightarrow {OB} .\overrightarrow {OM} (2) \cr  & M{C^2} = {\overrightarrow {MC} ^2} = 2{R^2} - 2\overrightarrow {OC.} \overrightarrow {OM} (3) \cr}$

Từ (1), (2) và (3) suy ra:

 $M{A^2} + M{B^2} + M{C^2}$$= 6{R^2} - 2\overrightarrow {OM} (\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )$

$O$ cũng là trọng tâm của tam giác $ABC$ nên $\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} = \overrightarrow  0$

Suy ra $M{A^2} + M{B^2} + M{C^2} = 6{R^2}$

Áp dụng định lý sin trong tam giác ABC ta có:

$\dfrac{a}{{\sin A}} = 2R$ $\Leftrightarrow \dfrac{a}{{\sin {{60}^0}}} = 2R$ $\Leftrightarrow R = \dfrac{a}{{2\sin {{60}^0}}} = \dfrac{a}{{2.\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{a\sqrt 3 }}{3}$

Vậy $M{A^2} + M{B^2} + M{C^2}$$= 6.{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2}= 2a^2$

LG b

Cho đường thẳng $d$ tùy ý, tìm điểm $N$ trên đường thẳng $d$ sao cho $NA^2+ NB^2 + NC^2$ nhỏ nhất.

Lời giải chi tiết:

$\begin{array}{l} N{A^2} + N{B^2} + N{C^2}\\ = {\overrightarrow {NA} ^2} + {\overrightarrow {NB} ^2} + {\overrightarrow {NC} ^2}\\ = {\left( {\overrightarrow {NO} + \overrightarrow {OA} } \right)^2} + {\left( {\overrightarrow {NO} + \overrightarrow {OB} } \right)^2} \\+ {\left( {\overrightarrow {NO} + \overrightarrow {OC} } \right)^2}\\ = {\overrightarrow {NO} ^2} + 2\overrightarrow {NO} .\overrightarrow {OA} + {\overrightarrow {OA} ^2}\\ + {\overrightarrow {NO} ^2} + 2\overrightarrow {NO} .\overrightarrow {OB} + {\overrightarrow {OB} ^2}\\ + {\overrightarrow {NO} ^2} + 2\overrightarrow {NO} .\overrightarrow {OC} + {\overrightarrow {OC} ^2}\\ = 3N{O^2} + 2\overrightarrow {NO} \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\\ + \left( {O{A^2} + O{B^2} + O{C^2}} \right)\\ = 3N{O^2} + 3{R^2} \end{array}$

(vì $\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0$ và $OA = OB = OC = R$)

Vì $R$ không đổi nên để $N{A^2} + N{B^2} + N{C^2}$ nhỏ nhất thì $NO$ nhỏ nhất hay N là hình chiếu của O trên d.

Vậy N là hình chiếu của O trên d thì $N{A^2} + N{B^2} + N{C^2}$ nhỏ nhất.

Loigiaihay.com