Câu 28 trang 119 Sách bài tập Hình học 11 Nâng cao

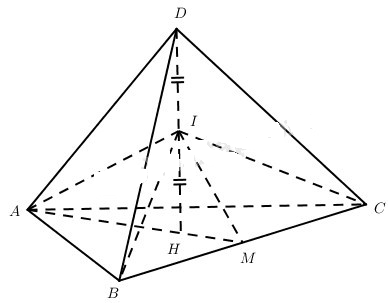
Đề bài

a) Cho tứ diện DABC có các cạnh bằng nhau. Gọi H là hình chiếu của D trên mp(ABC) và I là trung điểm của DH. Chứng minh rằng tứ diện IABC có IA, IB, IC đôi một vuông góc.

b) Cho tứ diện IABC có IA = IB = IC và IA, IB, IC đôi một vuông góc; H là hình chiếu của I trên mp(ABC). Gọi D là điểm đối xứng của H qua I. Chứng minh tứ diện DABC có các cạnh bằng nhau.

Lời giải chi tiết

a) Kí hiệu cạnh của tứ diện đã cho là a, dễ thấy H là trọng tâm của tam giác ABC. Từ đó

\(\eqalign{  & D{H^2} = D{A^2} - A{H^2}  \cr  &  = {a^2} - {\left( {{{a\sqrt 3 } \over 3}} \right)^2} = {{6{{\rm{a}}^2}} \over 9}  \cr  &  \Rightarrow DH = {{a\sqrt 6 } \over 3} \cr} \)

Do I là trung điểm của DH nên

\(IH = {{a\sqrt 6 } \over 6}\)

Khi đó: \(I{M^2} = I{H^2} + H{M^2} = {\left( {{{a\sqrt 6 } \over 6}} \right)^2} + {\left( {{{a\sqrt 3 } \over 6}} \right)^2} = {{{a^2}} \over 4}\),

tức là \(IM = {a \over 2}\).

Xét tam giác IBC có IM là trung tuyến \(IM = {1 \over 2}BC\). Vậy \(IB \bot IC\).

Tương tự như trên, ta có IA, IB, IC đôi một vuông góc.

b) Vì IA, IB, IC đôi một vuông góc, IA = IB = IC và H là hình chiếu của I trên mặt phẳng (ABC) nên ABC là tam giác đều nhận H làm trọng tâm.

Ngoài ra \({1 \over {I{H^2}}} = {1 \over {I{A^2}}} + {1 \over {I{B^2}}} + {1 \over {I{C^2}}} = {3 \over {I{A^2}}}\) hay \(IH = {{IA} \over {\sqrt 3 }}\).

Do D là điểm đối xứng của H qua I nên:

\(DH = {{2IA} \over {\sqrt 3 }}\) và DA = DB = DC.

Đặt IA = x thì \(DH = {{2{\rm{x}}} \over {\sqrt 3 }},AB = x\sqrt 2 \).

Khi đó

\(\eqalign{  & D{A^2} = D{H^2} + H{A^2} = {{4{x^2}} \over 3} + {\left( {{{x\sqrt 2 .\sqrt 3 } \over 3}} \right)^2}  \cr  &  = {{4{{\rm{x}}^2}} \over 3} + {{2{{\rm{x}}^2}} \over 3} = 2{{\rm{x}}^2} \cr} \).

Vậy \(DA = DB = DC = x\sqrt 2 \).

Do đó tứ diện DBCA có các cạnh bằng nhau.

Loigiaihay.com