Câu 19 trang 224 Sách bài tập Hình học 11 Nâng cao

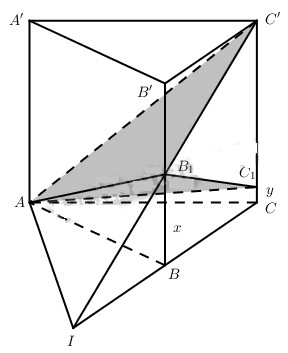
Đề bài

Cho hình lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a. Lấy điểm B₁ thuộc BB’, điểm C₁ thuộc CC’. Đặt \(B{B_1} = x,C{C_1} = y\).

a) Tam giác AB₁C₁ có thể vuông ở A được không? Tìm hệ thức liên hệ giữa a, x, y để AB₁C₁ là tam giác vuông tại B₁.

b) Giả sử AB₁C₁ là tam giác thường và B₁ là trung điểm của BB’, y = 2x và α là góc giữa mp(ABC) và mp(AB₁C₁). Hãy tính diện tích tam giác AB₁C₁ và độ dài cạnh bên của hình lăng trụ đã cho.

Lời giải chi tiết

 

a) ● Tam giác AB₁C₁ vuông ở A khi và chỉ khi

\({B_1}C_1^2 = AB_1^2 + AC_1^2\)

Mặt khác

\(\eqalign{  & {B_1}C_1^2 = {a^2} + {\left( {x - y} \right)^2}  \cr  & AB_1^2 = {a^2} + {x^2}  \cr  & AC_1^2 = {a^2} + {y^2} \cr} \)

Do đó tam giác AB₁C₁ vuông ở A khi và chỉ khi

\(\eqalign{  & {a^2} + {\left( {x - y} \right)^2} = 2{{\rm{a}}^2} + {x^2} + {y^2}  \cr  &  \Leftrightarrow 2{\rm{x}}y =  - {a^2} \cr} \)

Điều này không xảy ra. Vậy tam giác AB₁C₁ không thể vuông tại A được.

● Tam giác AB₁C₁ vuông tại B₁ khi và chỉ khi

\(\eqalign{  & AC_1^2 = AB_1^2 + {B_1}C_1^2  \cr  &  \Leftrightarrow {a^2} + {y^2} = {a^2} + {x^2} + {a^2} + {\left( {x - y} \right)^2}  \cr  &  \Leftrightarrow 2{\rm{x}}y = 2{{\rm{x}}^2} + {a^2} \cr} \)

Đó là hệt thức liên hệ giữa a, x, y để tam giác AB₁C₁ vuông tại B₁.

b) Khi B₁ là trung điểm của BB’, y =  2x thì C₁ trùng với C’.

Gọi \(I = BC \cap {B_1}C'\) thì \(AI = \left( {A{B_1}C'} \right) \cap \left( {ABC} \right)\).

Vì \({B_1}B = {1 \over 2}BB'\) nên BI =  BC, từ đó ta có IAC là tam giác vuông tại A, tức là \(AC \bot AI\).

Mặt khác, \(C'C \bot \left( {ABC} \right)\) nên \(AC' \bot AI\) (định lí ba đường vuông góc).

Như vậy \(\widehat {C'AC}\) là góc giữa mp(AB₁C’) và mp(ABC).

Theo giả thiết thì \(\widehat {C'AC} = \alpha \)

Từ đó \({S_{ABC}} = {S_{A{B_1}{C_1}}}\cos \alpha \)

tức là \({S_{A{B_1}{C_1}}} = {{{S_{ABC}}} \over {\cos \alpha }}\)

Như vậy \({S_{A{B_1}{C_1}}} = {{{a^2}\sqrt 3 } \over {4\cos \alpha }}\)

Ta có: \(CC' = AC\tan \alpha  = a\tan \alpha \)

Vậy độ dài cạnh bên của hình lăng trụ đã cho là \(a\tan \alpha \).

Loigiaihay.com