Câu 18 trang 224 Sách bài tập Hình học 11 Nâng cao

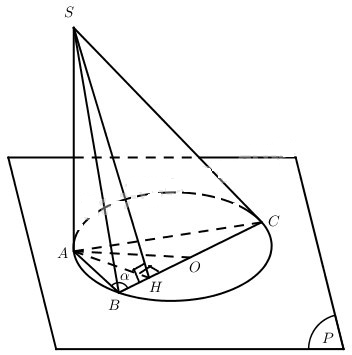
Đề bài

Trong mặt phẳng (P) cho đường tròn tâm O, bán kính R. Điểm A cố định thuộc đường tròn, đường kính BC quay quanh O, (BC không trùng với OA). Đặt \(\widehat {ABC} = \alpha \). Điểm S nằm trong không gian sao cho SA vuông góc với (P) và SA = 2R.

a) Chứng minh rằng chân đường cao SH của tam giác SBC thuộc một đường tròn cố định.

b) Xác định α để diện tích tam giác SBC đạt giá trị lớn nhất, hãy tính giá trị đó.

Lời giải chi tiết

a) Vì \(SA \bot \left( P \right)\) và \(SH \bot BC\) nên \(AH \bot BC\) (định lí ba đường vuông góc) hay \(\widehat {AHO} = {90^0}\). Như vậy H thuộc đường tròn đường kính AO trong mp(P). Đường tròn này cố định.

b) \({S_{SBC}} = {1 \over 2}BC.SH = R.SH\)

Do đó S_SBC lớn nhất khi và chỉ khi SH lớn nhất. Điều này xảy ra khi và chỉ khi AH lớn nhất, tức là H và O trùng nhau, khi đó \(\alpha  = {45^0}\).

Khi \(\alpha  = {45^0}\) thì \({S_{SBC}} = R.\sqrt {4{{\rm{R}}^2} + {R^2}}  = {R^2}\sqrt 5 \).

Loigiaihay.com