Bài 15 trang 30 SGK Hình học 10Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ. Quảng cáo
Đề bài Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào sau đây là đúng? A) \(|\overrightarrow {OA} + \overrightarrow {OB} | = AB\) B) \(\overrightarrow {OA} - \overrightarrow {OB} \) và \(\overrightarrow {DC}\) cùng hướng C) \({x_A} = - {x_C}\) và \({y_A} = {y_C}.\) D) \({x_B} = - {x_C}\) và \({y_C} =- {y_B}.\) Video hướng dẫn giải Lời giải chi tiết
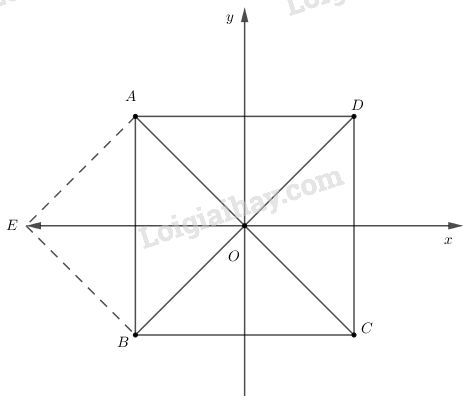
A) Ta có: \(\begin{array}{l} A đúng. B) Vì \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) Mà \(\overrightarrow {BA} \) và \(\overrightarrow {DC} \) ngược hướng nên B) sai C) Vì \({x_A} = - {x_C},\;\;y{ _A} = - {y_C} \Rightarrow C\) sai. D) Vì \({x_B} = - {x_C},\;\;{y_B} = {y_C} \Rightarrow D\) sai. Chọn A. Cách giải thích khác: Qua A kẻ \(\overrightarrow {AE} = \overrightarrow {OB} \)\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AE}\)\( = \overrightarrow {OE} \) Ta dễ dàng chứng minh được: \(\overrightarrow {OE} = \overrightarrow {DA} \Rightarrow |\overrightarrow {OA} + \overrightarrow {OB} |= |\overrightarrow {OE} |\)\( =|\overrightarrow {DA} |= |\overrightarrow {BA} | = AB\) Vậy A) đúng. Loigiaihay.com
|




















Danh sách bình luận