Các dạng toán về ứng dụng của tích phân trong hình họcCác dạng toán về ứng dụng của tích phân trong hình học Quảng cáo
1. Ứng dụng của tích phân trong hình học (diện tích hình phẳng) Dạng 1: Tính diện tích hình phẳng nếu biết hai đường giới hạn Phương pháp: - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) được tính bởi công thức: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \) - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\)được tính bởi công thức: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) Dạng 2: Tính diện tích hình phẳng nếu chưa biết hai đường giới hạn Phương pháp: - Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm. - Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\) - Bước 3: Tính diện tích hình phẳng theo công thức tích phân: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 2}}$ và các trục tọa độ. Chọn kết quả đúng nhất. A. $3\ln 6$ B. \(3\ln \dfrac{3}{2}\) C. \(3\ln \dfrac{3}{2} - 2\) D.\(3\ln \dfrac{3}{2} - 1\) Giải: Đồ thị hàm số cắt $Ox$ tại $\left( {-1;0} \right)$, cắt $Oy$ tại $\left( {0; - \dfrac{1}{2}} \right)$. Hàm số $y = \dfrac{{x + 1}}{{x - 2}}$ có \(y' = \dfrac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \in \left( { - 1;0} \right)\) nên hàm số $y = \dfrac{{x + 1}}{{x - 2}}$ nghịch biến trên $\left( {-1;0} \right)$. Do đó \(y < 0,\forall x \in \left( { - 1;0} \right)\) Do đó $S = \int\limits_{ - 1}^0 {\left| {\dfrac{{x + 1}}{{x - 2}}} \right|} dx = \int\limits_{ - 1}^0 {\left( { - \dfrac{{x + 1}}{{x - 2}}} \right)} dx = - \int\limits_{ - 1}^0 {\left( {1 + \dfrac{3}{{x - 2}}} \right)} dx $ $= - \left( {x + 3\ln \left| {x - 2} \right|\mathop |\nolimits_{ - 1}^0 } \right) = - 3\ln 2 - 1 + 3\ln 3 = 3\ln \dfrac{3}{2} - 1$ Chọn D. 2. Ứng dụng của tích phân trong hình học (thể tích vật thể) Dạng 1: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) quanh trục \(Ox\) Công thức tính: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \) Dạng 2: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(x = f\left( y \right)\), trục \(Oy\) và hai đường thẳng \(y = a,y = b\left( {a < b} \right)\) quanh trục \(Oy\). Công thức tính: \(V = \pi \int\limits_a^b {{f^2}\left( y \right)dy} \) Dạng 3: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right],0 \le f\left( x \right) \le g\left( x \right),\forall x \in \left[ {a;b} \right]\) quay quanh trục \(Ox\) Công thức tính: \(V = \pi \int\limits_a^b {\left[ {{g^2}\left( x \right) - {f^2}\left( x \right)} \right]dx} \) Dạng 4 ( Đọc thêm ): Tính thể tích của vật thể giới hạn bởi các mặt phẳng \(x = a,x = b\) biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục $Ox$ là \(S = S\left( x \right)\). Công thức tính: \(V = \int\limits_a^b {S\left( x \right)dx} \) Chú ý:
Khi miền \(D\) giới hạn bởi nhiều đồ thị hàm số thì ta nên vẽ hình, sau đó từ hình vẽ suy ra cách tính. Ví dụ: Cho đường cong \(y = - {x^2} + 1\) và đường thẳng \(y = 0\). Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi hai đường trên quanh \(Ox\). Ta có: \( - {x^2} + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right.\) 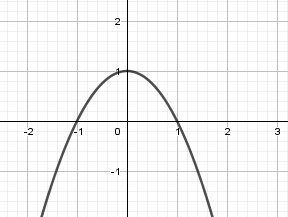 Thể tích: \(V = \pi \int\limits_{ - 1}^1 {{{\left( { - {x^2} + 1} \right)}^2}dx} = \pi \int\limits_{ - 1}^1 {\left( {{x^4} - 2{x^2} + 1} \right)dx} \) $= \pi \left. {\left( {\dfrac{{{x^5}}}{5} - \dfrac{{2{x^3}}}{3} + x} \right)} \right|_{ - 1}^1 = \dfrac{{16\pi }}{{15}}$.
|




















Danh sách bình luận