Giải bài 3 trang 121 SGK Giải tích 12

Đề bài

Parabol \(y = {{{x^2}} \over 2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt2\) thành hai phần. Tìm tỉ số diện tích của chúng.

Lời giải chi tiết

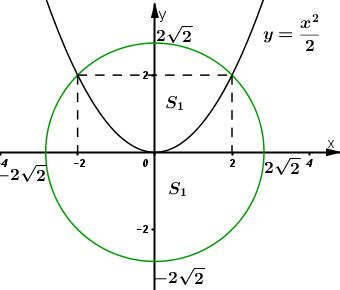
Đường tròn đã cho có phương trình: \({x^{2}} + {\rm{ }}{y^2} = {\rm{ }}8.\)

Từ đó ta có: \(y =  \pm \sqrt {8 - {x^2}} \)

Tọa độ giao điểm của \((C)\) và \((P)\) là nghiệm của hệ phương trình: 

\(\left\{ \matrix{
{x^2} = 2y \hfill \cr
{x^2} + {y^2} = 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{y^2} + 2y - 8 = 0 \hfill \cr
{x^2} = 2y \hfill \cr} \right.\)

\( \Leftrightarrow \left\{ \matrix{ \left[ \begin{array}{l} y = 2\;\;\left( {tm} \right)\\y = - 4\;\;\left( {ktm} \right)\end{array} \right. \hfill \cr x^2=2y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{y = 2 \hfill \cr x = \pm 2 \hfill \cr} \right.\)

Gọi \(S_1\) và \(S_2\) là diện tích hai phần của đường tròn được chia bởi parabol \((P)\) như hình vẽ.

Khi đó ta có:

\(\begin{array}{l}{S_1} = \int\limits_{ - 2}^2 {\left( {\sqrt {8 - {x^2}}  - \frac{{{x^2}}}{2}} \right)dx} \\ = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} dx}  - \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx} \\ = {I_1} - {I_2}\end{array}\)

Tính \({I_1} = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} dx} \)

Đặt \(x = 2\sqrt 2 \sin t \Rightarrow dx = 2\sqrt 2 {\mathop{\rm costdt}\nolimits} \)

Đổi cận:

\(\eqalign{
& x = -2 \Rightarrow t = -{\pi \over 4} \cr
& x = 2 \Rightarrow t = {\pi \over 4} \cr} \)

\(\begin{array}{l}{I_1} = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8 - 8{{\sin }^2}t} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8\left( {1 - {{\sin }^2}t} \right)} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8{{\cos }^2}t} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {2\sqrt 2 \cos t.2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {8{{\cos }^2}tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {8.\frac{{1 + \cos 2t}}{2}dt} \\ = 4\int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt} \\ = 4\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_{ - \frac{\pi }{4}}^{\frac{\pi }{4}}\\ = 4\left( {\frac{\pi }{4} + \frac{{\sin \frac{\pi }{2}}}{2} + \frac{\pi }{4} - \frac{{\sin \left( { - \frac{\pi }{2}} \right)}}{2}} \right)\\ = 2\pi  + 4\end{array}\)

Tính \({I_2} = \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx} \)

\(\begin{array}{l}{I_2} = \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx}  = \frac{1}{2}.\left. {\frac{{{x^3}}}{3}} \right|_{ - 2}^2\\ = \frac{1}{2}\left( {\frac{8}{3} - \frac{{ - 8}}{3}} \right) = \frac{8}{3}\end{array}\)

Do đó \({S_1} = {I_1} - {I_2} = 2\pi  + 4 - \frac{8}{3} = 2\pi  + \frac{4}{3}\)

Diện tích hình tròn là: \(\pi R^2=8\pi\)

\({S_2} = 8\pi  - {S_1}\)\(= 8\pi-2\pi  - {4 \over 3}=6\pi-{4\over 3}.\)

Vậy \({{{S_2}} \over {{S_1}}} = \frac{{6\pi  - \frac{4}{3}}}{{2\pi  + \frac{4}{3}}} = \frac{{18\pi  - 4}}{{6\pi  + 4}} = {{9\pi  - 2} \over {3\pi  + 2}}\) hay \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{3\pi  + 2}}{{9\pi  - 2}}\)

Loigiaihay.com