Bài tập cuối tuần Toán 4 tuần 23 - Đề 2 (Có đáp án và lời giải chi tiết)

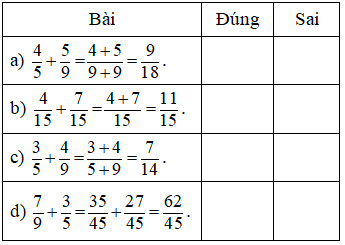
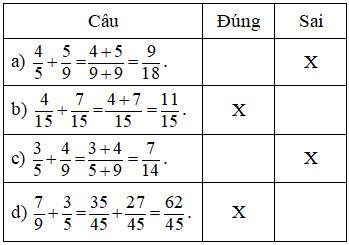
Đề bài

Bài 1. Đánh dấu X vào ô thích hợp 

Bài 2.  Tính

a) \(\dfrac{4}{5}\; + \;\dfrac{3}{8}\) = …………………………......

b) \(\dfrac{5}{9}\; + \;\dfrac{{21}}{{45}}\) = ……………………….........

c) \(\dfrac{1}{6}\; + \;\dfrac{5}{8}\) = ……………………………

Bài 3. Rút gọn rồi tính :

a) \(\dfrac{{22}}{{55}} + \;\dfrac{{25}}{{125}}\) = ……………………........

b) \(\dfrac{{22}}{{77}} + \;\dfrac{{56}}{{98}} + \;\dfrac{{25}}{{105}}\;\) =………………………………

Bài 4. Tính nhanh

a)\(\;\dfrac{8}{{27\;}} + \;\dfrac{4}{{15}} + \;\dfrac{{19}}{{27}} + \;\dfrac{{11}}{{15}}\)

……………………………………………………………………………………..............

……………………………………………………………………………………..............

b) \(\dfrac{{12}}{{13\;}} + \;\dfrac{2}{7} + \;\dfrac{8}{{13}} + \;\dfrac{6}{{13}} + \dfrac{5}{7}\)

……………………………………………………………………………………..............

……………………………………………………………………………………..............

Bài 5. Viết các phân số sau thành tổng ba phân số có tử số là 1 và mẫu số khác nhau :

a) \(\dfrac{{13}}{{35}}\) = .…………………………………

b) \(\dfrac{{17}}{{63}}\) =  …………………………………

Bài 6. Sau khi bớt ở phân số thứ nhất đi \(\dfrac{1}{5}\) thì tổng hai phân số là \(\dfrac{7}{9}\).  Tính tổng hai phân số ban đầu.

Bài giải

........................................................................................................................................

........................................................................................................................................

........................................................................................................................................

Lời giải chi tiết

Bài 1.

Phương pháp:

- Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.

- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Cách giải:

Ta có:

\(\begin{array}{l}a)\,\,\dfrac{4}{5} + \dfrac{5}{9} = \dfrac{{36}}{{45}} + \dfrac{{25}}{{45}} = \dfrac{{61}}{{45}};\\b)\dfrac{4}{{15}} + \dfrac{7}{{15}} = \dfrac{{4 + 7}}{{15}} = \dfrac{{11}}{{15}};\\c)\dfrac{3}{5} + \dfrac{4}{9} = \dfrac{{27}}{{45}} + \dfrac{{20}}{{45}} = \dfrac{{47}}{{45}};\\d)\dfrac{7}{9} + \dfrac{3}{5} = \dfrac{{35}}{{45}} + \dfrac{{27}}{{45}} = \dfrac{{62}}{{45}}.\end{array}\)

Vậy ta có kết quả như sau: 

Bài 2.

Phương pháp:

Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Cách giải:

a) \(\dfrac{4}{5}\; + \;\dfrac{3}{8} = \dfrac{{32}}{{40}} + \dfrac{{15}}{{40}} = \dfrac{{47}}{{40}};\)

b) \(\dfrac{5}{9}\; + \;\dfrac{{21}}{{45}} = \dfrac{{25}}{{45}} + \dfrac{{21}}{{45}} = \dfrac{{46}}{{45}};\)

c) \(\dfrac{1}{6}\; + \;\dfrac{5}{8} = \dfrac{4}{{24}} + \dfrac{{15}}{{24}} = \dfrac{{19}}{{24}}.\)

Bài 3.

Phương pháp:

- Rút gọn phân số thành phân số tối giản (nếu được).

- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Cách giải:

a) \(\dfrac{{22}}{{55}} + \dfrac{{25}}{{125}} = \dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5};\)

b) \(\dfrac{{22}}{{77}} + \dfrac{{56}}{{98}} + \dfrac{{25}}{{105}} = \dfrac{2}{7} + \dfrac{4}{7} + \dfrac{5}{{21}}\)\( = \dfrac{6}{7} + \dfrac{5}{{21}} = \dfrac{{18}}{{21}} + \dfrac{5}{{21}} = \dfrac{{23}}{{21}}.\)

Bài 4.

Phương pháp:

Áp dụng tín chất giao hoán và kết hợp của phép cộng để ghép các phân số có cùng mẫu số lại thành một nhóm để tính thuận tiện hơn.

Cách giải:

\(\begin{array}{l}a)\,\,\;\dfrac{8}{{27\;}} + \;\dfrac{4}{{15}} + \;\dfrac{{19}}{{27}} + \;\dfrac{{11}}{{15}}\\\,\,\,\,\,\, = \left( {\dfrac{8}{{27}} + \dfrac{{19}}{{27}}} \right) + \left( {\dfrac{4}{{15}} + \dfrac{{11}}{{15}}} \right)\\\,\,\,\,\,\, = \dfrac{{27}}{{27}} + \dfrac{{15}}{{15}}\\\,\,\,\,\,\, = \,\,\,1 + 1\\\,\,\,\,\,\, = \,\,\,\,\,\,2\end{array}\)

\(\begin{array}{l}b)\,\,\,\dfrac{{12}}{{13\;}} + \;\dfrac{2}{7} + \;\dfrac{8}{{13}} + \;\dfrac{6}{{13}} + \dfrac{5}{7}\\\,\,\,\,\,\, = \left( {\dfrac{{12}}{{13}} + \dfrac{8}{{13}} + \dfrac{6}{{13}}} \right) + \left( {\dfrac{2}{7} + \dfrac{5}{7}} \right)\\\,\,\,\,\,\, = \dfrac{{26}}{{13}} + \dfrac{7}{7}\\\,\,\,\,\,\, = \,\,2 + 1\\\,\,\,\,\,\, = \,\,\,\,\,\,3\end{array}\)

Bài 5.

Phương pháp:

Viết mỗi phân số đã cho thành tổng của 3 phân số, sau đó rút gọn các phân số để được phân số có tử số là 1 (nếu được).

Cách giải:

a) \(\dfrac{{13}}{{35}} = \dfrac{1}{{35}} + \dfrac{7}{{35}} + \dfrac{5}{{35}}\)\( = \dfrac{1}{{35}} + \dfrac{1}{5} + \dfrac{1}{7}.\)

b) \(\dfrac{{17}}{{63}} = \dfrac{1}{{63}} + \dfrac{9}{{63}} + \dfrac{7}{{63}}\)\( = \dfrac{1}{{63}} + \dfrac{1}{7} + \dfrac{1}{9}.\)

Bài 6.

Phương pháp:

Nếu bớt ở phân số thứ nhất đi \(\dfrac{1}{5}\) thì tổng của hai phân số ban đầu cũng giảm đi \(\dfrac{1}{5}\).

Do đó, để tìm tổng ban đầu ta lấy tổng mới cộng với \(\dfrac{1}{5}.\)

Cách giải:

Sau khi bớt ở phân số thứ nhất đi \(\dfrac{1}{5}\) thì tổng của 2 phân số ban đầu cũng giảm đi \(\dfrac{1}{5}.\)

Vậy tổng hai phân số ban đầu là :

                  \(\dfrac{7}{9} + \;\dfrac{1}{5} = \;\dfrac{{44}}{{45}}\).

                           Đáp số: \(\;\dfrac{{44}}{{45}}\).

Loigiaihay.com