Bài tập 22 trang 105 Tài liệu dạy – học Toán 8 tập 1

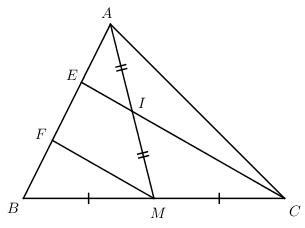
Đề bài

Cho tam giác nhọn ABC, kẻ trung tuyến AM. Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh rằng:

a) EF = FB;

b) \(AE = {1 \over 3}AB\)

c) CE = 4EI.

Lời giải chi tiết

a) Xét tam giác BEC có : MF // EC (gt)

Và M là trung điểm của BC (gt)

\( \Rightarrow F\) là trung điểm của BE \( \Rightarrow EF = BF\)

b) Xét tam giác AMF có: EI // MF (gt)

Và I là trung điểm của AM (gt)

\( \Rightarrow E\) là trung điểm của AF \( \Rightarrow AE = EF\)

Mà \(EF = BF\) nên \(AE = EF = BF \Rightarrow AE = {1 \over 3}AB\)

c) Xét tam giác EBC ta có :

M là trung điểm của BC (gt) ;

F là trung điểm của BE ;

\( \Rightarrow MF\) là đường trung bình của tam giác EBC \( \Rightarrow MF = {1 \over 2}EC\)

Xét \(\Delta AMF\) ta có:

E là trung điểm của AF (gt);

I là trung điểm của AM (gt) ;

\( \Rightarrow EI\) là đường trung bình của tam giác AMF

\( \Rightarrow EI = {1 \over 2}MF\)

Mà \(MF = {1 \over 2}EC\)

\( \Rightarrow EI = {1 \over 2}.{1 \over 2}EC = {1 \over 4}EC \Rightarrow EC = 4EI\)

Loigiaihay.com