Bài 9 trang 119 SGK Hình học 10 nâng cao

LG a

Viết phương trình của các tiếp tuyến của (C) kể từ A.

Lời giải chi tiết:

Đường tròn (C) có tâm  O(0 ; 0), bán kính R=2.

+ Đường thẳng Δ qua A và nhận \(\overrightarrow n  = \left( {a;b} \right)\) làm VTPT có dạng

\(\eqalign{
& a(x + 2) + b(y - 3) = 0 \cr 
& \Leftrightarrow \,ax + by + 2a - 3b = 0 \cr} \) 

Δ là tiếp tuyến của (C)

\(\eqalign{
& \Leftrightarrow \,\,d(O\,;\,\Delta ) = R\cr & \Leftrightarrow \,\,\,{{|2a - 3b|} \over {\sqrt {{a^2} + {b^2}} }} = 2 \cr 
& \Leftrightarrow \,\,{(2a - 3b)^2} = 4({a^2} + {b^2}) \cr 
& \Leftrightarrow 4{a^2} - 12ab + 9{b^2} = 4{a^2} + 4{b^2}\cr &\Leftrightarrow \,\,5{b^2} - 12ab = 0 \cr 
& \Leftrightarrow \,\,b(5b - 12a) = 0\cr&\Leftrightarrow \left[ \matrix{
b = 0 \hfill \cr 
12a = 5b \hfill \cr} \right. \cr} \) 

Với b = 0, chọn a = 1 ta có tiếp tuyến \({\Delta _1}\,\,:\,\,x + 2 = 0\)

Với \(12a=5b\), chọn \(a=5, b=12\) ta có tiếp tuyến \({\Delta _2}:\,\,5x + 12y - 26 = 0\)

LG b

Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.

Lời giải chi tiết:

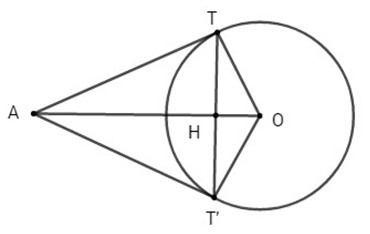
Gọi T, T’ là tiếp điểm của \({\Delta _1}\,,\,{\Delta _2}\) với (C) . Ta có

\(AT = AT' = \sqrt {A{O^2} - {R^2}}  \) \(= \sqrt {13 - 4}  = 3\)

Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có

\(\eqalign{
& {1 \over {T{H^2}}} = {1 \over {A{T^2}}} + {1 \over {T{O^2}}} \cr &= {1 \over 9} + {1 \over 4} = {{13} \over {36}} \cr 
& \Rightarrow \,\,TH = {6 \over {\sqrt {13} }}\,\cr & \Rightarrow TT' = 2TH = {{12} \over {\sqrt {13} }} \cr} \)

Loigiaihay.com