Bài 10 trang 119 SGK Hình học 10 nâng cao

LG a

Tìm tọa độ các tiêu điểm của (E) và (H).

Lời giải chi tiết:

Với \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) ta có:

\({a^2} = 5,{b^2} = 4\) \(\Rightarrow a = \sqrt 5 ,b = 2\)

\(\Rightarrow \,c = \sqrt {{a^2} - {b^2}}  = 1\)

Tọa độ các tiêu điểm của (E) là \({F_1}( - 1\,;\,0)\,,\,\,{F_2}(1\,;\,0)\)

Với (H) : \({{{x^2}} \over 5} - {{{y^2}} \over 4} = 1\) , ta có:

\({a^2} = 5,{b^2} = 4\) \(\Rightarrow a = \sqrt 5 ,b = 2\)

\(\Rightarrow \,c = \sqrt {{a^2} + {b^2}}  = 3\)

Tọa độ các tiêu điểm của (H) là \({F_1'}( - 3\,;\,0)\,,\,\,{F_2'}(3\,;\,0)\)

LG b

Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.

Lời giải chi tiết:

Vẽ (E) và (H).

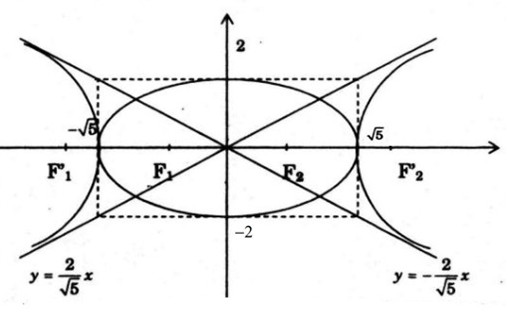
(E ) nhận Ox, Oy làm hai trục đối xứng

\({F_1}( - 1\,;\,0)\,,\,\,{F_2}(1\,;\,0)\) làm tiêu điểm

Cắt Ox tại \(\left( { - \sqrt 5 ;0} \right),\left( {\sqrt 5 ;0} \right)\) và cắt Oy tại \(\left( {0; - 2} \right),\left( {0;2} \right)\)

(H) nhận \({F_1'}( - 3\,;\,0)\,,\,\,{F_2'}(3\,;\,0)\) làm tiêu điểm, trục Ox, Oy là trục đối xứng

Các đường thẳng \(y =  \pm \frac{2}{{\sqrt 5 }}x\) là tiệm cận.

LG c

Tìm tọa độ các giao điểm của (E) và (H).

Lời giải chi tiết:

Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình

\(\left\{ \matrix{
{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1 \hfill \cr 
{{{x^2}} \over 5} - {{{y^2}} \over 4} = 1 \hfill \cr} \right.\) \(\Leftrightarrow \,\,\,\left\{ \matrix{
{x^2} = 5 \hfill \cr 
{y^2} = 0 \hfill \cr} \right.\) \( \Leftrightarrow \,\,\,\left\{ \matrix{
x = \pm \sqrt 5 \hfill \cr 
y = 0 \hfill \cr} \right.\) 

Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 \,;\,0} \right)\) và \(\left( -{\sqrt 5 \,;\,0} \right)\) .

Loigiaihay.com