Bài 88 trang 156 SGK Đại số 10 nâng caoTập nghiệm của bất phương trình là: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
LG a Tập nghiệm của bất phương trình: \((3 - 2\sqrt 2 ){x^2} - 2(3\sqrt 2 - 4) + 6(2\sqrt 2 - 3) \le 0\) là: \(\eqalign{ Lời giải chi tiết: Gọi \(f(x) = (3 - 2\sqrt 2 ){x^2} - 2(3\sqrt 2 - 4) + 6(2\sqrt 2 - 3)\) Vì ac < 0 nên f(x) có hai nghiệm phân biệt x1 < x2 Bảng xét dấu:
Loại trừ (B), (C) Ta có: \(f( - 2) = 2(3 - 2\sqrt 2 ) + 2\sqrt 2 (3\sqrt 2 - 4) \) \(+ 6(2\sqrt 2 - 3) = 0\) Vậy chọn A. Cách khác: LG b Tập nghiệm của bất phương trình: \((2 + \sqrt 7 ){x^2} + 3x - 14 - 4\sqrt 7 \ge 0\) là: \(\eqalign{ Lời giải chi tiết: Gọi \(f(x) = (2 + \sqrt 7 ){x^2} + 3x - 14 - 4\sqrt 7 \) Vì ac < 0 nên f(x) có hai nghiệm phân biệt x1 < x2 Bảng xét dấu:
Loại trừ (A), (C) Ta có: \(f(2) = 4(2 + \sqrt 7 ) + 6 - 14 - 4\sqrt 7 = 0\) Chọn (B) Cách khác: LG c Tập nghiệm của bất phương trình: \({{(x - 1)({x^3} - 1)} \over {{x^2} + (1 + 2\sqrt 2 )x + 2 + \sqrt 2 }} \le 0\) là: \(\eqalign{ Lời giải chi tiết: Gọi \(f(x) = {{(x - 1)({x^3} - 1)} \over {{x^2} + (1 + 2\sqrt 2 )x + 2 + \sqrt 2 }}\) Ta có: f(1) = 0 nên loại trừ (A) \(f(0) = {1 \over {2 + \sqrt 2 }} > 0\) nên loại trừ (B) f(2) > 0 nên loại trừ D Vậy chọn C. Cách khác: Loigiaihay.com
|















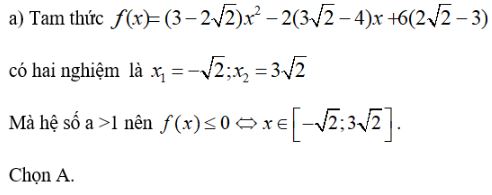


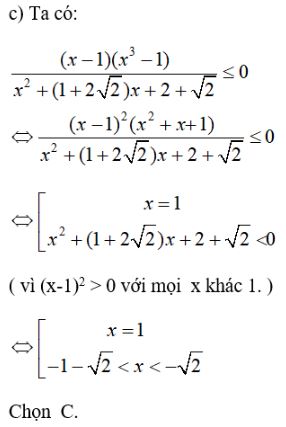






Danh sách bình luận