Bài 77 trang 62 SGK giải tích 12 nâng caoCho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1. b) Chứng minh rằng với mọi , các đường cong đều đi qua hai điểm cố định A và B. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
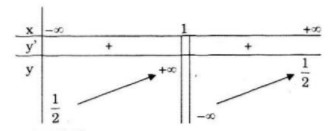
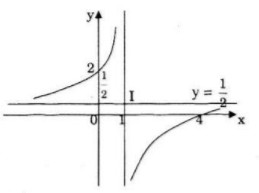
Cho hàm số: \(y = {{x - 4m} \over {2\left( {mx - 1} \right)}}.\,\,\,\left( {{H_m}} \right)\) LG a Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1. Lời giải chi tiết: Với m=1 hàm số có dạng: \(y = {{x - 4} \over {2x - 2}}\) Tập xác định: \(D = R\backslash \left\{ 1 \right\}\) \(y' = {6 \over {{{\left( {2x - 2} \right)}^2}}} > 0\,,\forall x \in D\) Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) Hàm số không có cực trị Giới hạn: \(\mathop {\lim y}\limits_{x \to {1^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = - \infty \) Đường tiệm cận đứng: \(x=1\) \(\mathop {\lim }\limits_{x \to \pm \infty } y = {1 \over 2}\) Đường tiệm cận ngang \(y={1 \over 2}\) Bảng biến thiên:
Đồ thị: Đồ thị giao Ox, Oy tại các điểm: (4;0); (0;2)
LG b Chứng minh rằng với mọi \(m \ne \pm {1 \over 2}\), các đường cong \(\left( {{H_m}} \right)\) đều đi qua hai điểm cố định A và B. Lời giải chi tiết: Gọi \(M\left( {{x_o};{y_o}} \right)\) là một điểm bất kì của mặt phẳng tọa độ. Đường cong \(\left( {{H_m}} \right)\) đi qua điểm M khi và chỉ khi \((x_o;y_o)\) thỏa mãn \({{{x_o} - 4m} \over {2\left( {m{x_o} - 1} \right)}} = {y_o}\) \( \Leftrightarrow \left\{ \matrix{ Mọi đường cong \(\left( {{H_m}} \right)\) với \(m \ne \pm {1 \over 2}\) đều đi qua điểm \(M\left( {{x_o};{y_o}} \right)\) khi và chỉ khi hệ phương trình trên nghiệm đúng với mọi \(m \ne \pm {1 \over 2}\). Phương trình (2) nghiệm đúng với mọi m khi và chỉ khi \(\left\{ \matrix{ \( \Leftrightarrow \left\{ \begin{array}{l} \(\Leftrightarrow \left\{ \matrix{ Vậy \(\left( {{x_o};{y_o}} \right)\) =(-2;1) và \(\left( {{x_o};{y_o}} \right)\)=(2;-1) Ta kiểm tra điều kiện (1) •Với \({x_o} = 2\), ta có \(m \ne {1 \over 2}\) Vậy mọi đường cong \(\left( {{H_m}} \right)\) với \(m \ne \pm {1 \over 2}\) đều đi qua hai điểm cố định A(-2; 1) và B(2; - 1). LG c Chứng minh rằng tích các hệ số góc của tiếp tuyến với (\(H_m\)) tại hai điểm A và B là một hằng số khi m biến thiên. Lời giải chi tiết: Ta có \(y' = {{4{m^2} - 1} \over {2{{\left( {mx - 1} \right)}^2}}}\) Hệ số góc tiếp tuyến với \(\left( {{H_m}} \right)\) tại A(-2; 1) và \(B(2; - 1)\) là y’(-2) và y'(2). Ta có tích hai hệ số góc tiếp tuyến tại A và B là: \(y'\left( { - 2} \right).y'\left( 2 \right) \) \(= {{4{m^2} - 1} \over {2{{\left( {-2m - 1} \right)}^2}}}.{{4{m^2} - 1} \over {2{{\left( {2m - 1} \right)}^2}}} \) \(= {1 \over 4}\) là hằng số. Loigiaihay.com
|




















Danh sách bình luận