Bài 6 trang 51 SGK Hình học 10 nâng cao

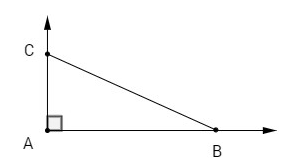
LG a

\(\cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\)

Phương pháp giải:

Xác định góc giữa các véc tơ đã cho và giá trị lượng giác của chúng.

Từ đó thay vào tính giá trị biểu thức.

Lời giải chi tiết:

Ta có: \(\widehat B = {30^0} \) \(\Rightarrow \widehat C = {90^0} - {30^0} = {60^0}\)

\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {150^0};(\overrightarrow {BA} ,\,\overrightarrow {BC} ) = {30^0},\) \((\overrightarrow {AC} ,\,\overrightarrow {CB} ) = {120^0}\)

Do đó

\(\eqalign{
& \cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\cr& = \cos {150^0} + {\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0} + \tan {60^0} \cr 
& = {{ - \sqrt 3 } \over 2} + {1 \over 2} + \sqrt 3 = {{\sqrt 3 + 1} \over 2} \cr} \)

LG b

\(\sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} )\)

Lời giải chi tiết:

Ta có \((\overrightarrow {CA} ,\,\overrightarrow {BA} ) = {90^0}\), do đó

\(\eqalign{
& \sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} ) \cr&= \sin {90^0} + \cos {30^0} + \cos {90^0} \cr 
&= 1 + {{\sqrt 3 } \over 2} + 0 = {{2 + \sqrt 3 } \over 2} \cr} \) 

Loigiaihay.com