Bài 10 trang 52 SGK Hình học 10 nâng caoCho hai điểm M, N nằm trên đường tròn đường kính AB = 2R Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
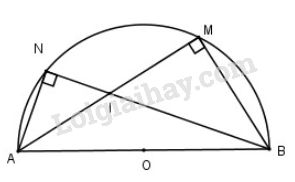
Cho hai điểm \(M, N\) nằm trên đường tròn đường kính \(AB = 2R\). Gọi \(I\) là giao điểm của hai đường thẳng \(AM, BN\). LG a Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI} \,\,;\,\,\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\) Phương pháp giải: Sửa dụng quy tắc ba điểm, xen điểm thích hợp và chú ý: \[\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\] Lời giải chi tiết:
AB là đường kính nên \(\widehat {AMB} = \widehat {ANB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \left\{ \begin{array}{l} Ta có: \({\overrightarrow {AI} .\overrightarrow {AM} } = \overrightarrow {AI} \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right) \) \(= \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {AI} .\overrightarrow {BM} \) Mặt khác: \(\overrightarrow {AI} \bot \overrightarrow {BM} \) (do AM\(\bot\) MB) nên \(\overrightarrow {AI} .\overrightarrow {BM} = 0\) Từ đó: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB} +0\) \(= \overrightarrow {AI} .\overrightarrow {AB}\) Hay \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI}\) Ta có: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} \left( {\overrightarrow {BA} + \overrightarrow {AN} } \right) \)\(= \overrightarrow {BI} .\overrightarrow {BA} + \overrightarrow {BI} .\overrightarrow {AN} \) Mặt khác: \(\overrightarrow {BI} \bot \overrightarrow {AN} \) (vì BN \(\bot\) NA) nên \(\overrightarrow {BI} .\overrightarrow {AN} = 0\) Từ đó: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} .\overrightarrow {BA} +0\)\(=\overrightarrow {BI} .\overrightarrow {BA}\). Hay \(\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\) LG b Tính \(\overrightarrow {AM} .\overrightarrow {AI} + \,\,\overrightarrow {BN} .\overrightarrow {BI} \) theo \(R\). Lời giải chi tiết: \(\eqalign{& \overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI}\cr& = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} \cr & = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\cr & = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {BI} .\overrightarrow {AB} \cr&= \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) \cr & = \overrightarrow {AB} .\left( {\overrightarrow {AI} + \overrightarrow {IB} } \right)\cr &= \overrightarrow {AB} .\overrightarrow {AB} = {\overrightarrow {AB} ^2} = 4{{\rm{R}}^2} \cr} \) Loigiaihay.com
|




















Danh sách bình luận