Bài 6 trang 46 Vở bài tập toán 9 tập 2

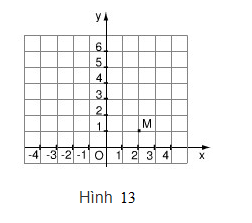
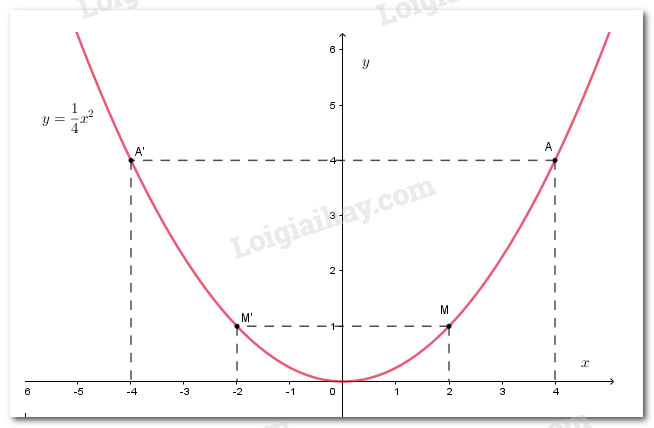
LG a

Tìm hệ số a

Phương pháp giải:

Thay tọa độ điểm M vào hàm số \(y = a{x^2}\) để tìm hệ số \(a.\)

Lời giải chi tiết:

Theo hình 13, tọa độ của điểm \(M\left( {2;1} \right)\) là một điểm thuộc đồ thị \(y = a{x^2}.\) Do đó, tọa độ của M phải thỏa mãn đẳng thức \(y = a{x^2}\) nghĩa là \(1 = a{.2^2}\) hay \(1 = 4a\). Vậy \(a = \dfrac{1}{4}\)

LG b

Điểm A(4 ; 4) có thuộc đồ thị không ?

Phương pháp giải:

Thay tọa độ điểm A vào hàm số tìm được để xác định xem A có thuộc đồ thị hay không?

Lời giải chi tiết:

Thay \(x = 4\) vào đẳng thức \(y = \dfrac{1}{4}{x^2}\), ta được \(y =\dfrac{1}{4}.{4^2}= 4\). Điều này chứng tỏ tọa độ của điểm A thỏa mãn đẳng thức \(y = \dfrac{1}{4}{x^2}\). Vậy điểm \(A\left( {4;4} \right)\) thuộc đồ thị hàm số \(y = \dfrac{1}{4}{x^2}.\)

LG c

Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.

Phương pháp giải:

Tìm thêm điểm dựa vào tính đối xứng qua trục tung của đồ thị, từ đó vẽ đồ thị hàm số tìm được.

Lời giải chi tiết:

Nhờ tính đối xứng của đồ thị qua Oy, không cần tính toán, có thể lấy thêm hai điểm \(M';A'\) lần lượt đối xứng với \(M;A\) qua Oy. Hai điểm \(M';A'\) cũng thuộc đồ thị.

Từ đó ta vẽ đồ thị đi qua 5 điểm \(A;M;O;M';A'\)  ta được đồ thị \(y = \dfrac{1}{4}{x^2}.\) 

Loigiaihay.com